Introduction
Short-rate martingale models were among the first approaches to the modelling of interest rate term structures, providing a flexible framework for pricing fixed-income securities and interest rate derivatives. These models describe the evolution of the continuous short rate as a stochastic process and are widely used in both theoretical and practical applications. A key class of such models are affine term structure models (ATSM), which allow for tractable pricing solutions without much computational efforts.
This primer explores and compares some of the most important short-rate models, including the Vasicek, Ho-Lee, Cox-Ingersoll-Ross (CIR), Hull-White (one-factor and two-factor) models. First, we derive the affine term structure pricing partial differential equation (PDE) governing these models and examine their implications for bond pricing. Furthermore, we discuss techniques for their calibration to observed market prices and their application to the valuation of interest rate derivatives such as bond options, caps, floors, and swaptions. By comparing these models, we highlight their strengths and limitations in capturing real-world interest rate dynamics and their suitability for practical financial applications.
Basic assumptions and definitions:
Before diving into the models, let us first define the underlying assumptions and definitions used. Let us denote by P(t,T) the price of a zero coupon bond (ZCB) with notional 1 at time t with maturity T. Furthermore, define a term structure as given by p(t,T) as a function of T for all T for a fixed value of t. We assume that there exists a (frictionless) market for ZCBs for every T > 0 (i.e. infinite amount of different bonds with different T). The relation p(t,t) = 1 holds for all t to avoid arbitrage (at maturity T, bonds experience a pull to par). We thus ignore the potential of premature default. The market is also assumed to be arbitrage-free and for each fixed t, the bond price p(t,T) is differentiable with respect to time of maturity T. Furthermore, let us also define the continuously compounded forward rate for [S,T] contracted at t as: ![]() , the continuously compounded spot rate for [S,T] as:
, the continuously compounded spot rate for [S,T] as: ![]() , the instantaneous forward rate (riskless rate of interest, contracted at t, over the infinitesimal interval [T,T+dT]) as:
, the instantaneous forward rate (riskless rate of interest, contracted at t, over the infinitesimal interval [T,T+dT]) as: ![]() , and the instantaneous short rate at t as:
, and the instantaneous short rate at t as:
![]() . Our market also has an exogenous asset (with short rate r given) called the locally risk-free money account which follows the process:
. Our market also has an exogenous asset (with short rate r given) called the locally risk-free money account which follows the process:
![]()
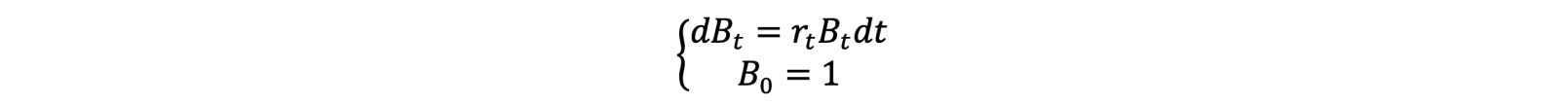
In general, ![]() is assumed to be stochastic with the following general dynamics under the risk neutral measure Q:
is assumed to be stochastic with the following general dynamics under the risk neutral measure Q:
![]()
with drift term ![]() , diffusion term
, diffusion term ![]() and W being a Q-Wiener process representing the risk factor. Now, the term structure is completely determined by specifying the short rate dynamics under the martingale measure Q as the short rate is the process driving bond prices via the risk-neutral ZCB pricing formula:
and W being a Q-Wiener process representing the risk factor. Now, the term structure is completely determined by specifying the short rate dynamics under the martingale measure Q as the short rate is the process driving bond prices via the risk-neutral ZCB pricing formula:
![]()
With ![]() and F being a smooth function of three real variables. It therefore becomes clear that whenever one can characterize the distribution of
and F being a smooth function of three real variables. It therefore becomes clear that whenever one can characterize the distribution of ![]() in terms of chosen dynamics for r, conditional on the information available at time t, one is able to compute bond prices
in terms of chosen dynamics for r, conditional on the information available at time t, one is able to compute bond prices ![]() . Knowing the term structure and the dynamics of the short rate one can then also price other interest rate derivatives.
. Knowing the term structure and the dynamics of the short rate one can then also price other interest rate derivatives.
Term structure PDE and affine term structure models:
By building a locally risk-free portfolio consisting of two ZCBs with different maturities, imposing no arbitrage conditions and applying Ito’s lemma a general term structure PDE can be obtained by a similar approach to the one of the famous Black-Scholes PDE [1]:
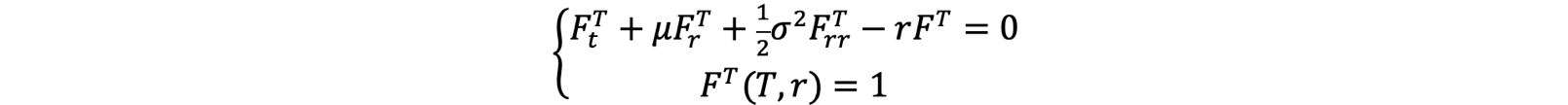
where ![]() represents the pricing function of a ZCB and
represents the pricing function of a ZCB and ![]() the pull to par boundary condition at bond maturity.
the pull to par boundary condition at bond maturity.
Let us now define the special case where we can write ![]() as an affine term structure. For a model to follow an affine term structure A(t, T) and B(t, T) must be deterministic functions. Given the previously defined risk neutral dynamics of the short rate, we can insert the affine term structure expression in the general term structure PDE to obtain an affine pricing PDE and determine the following boundary conditions:
as an affine term structure. For a model to follow an affine term structure A(t, T) and B(t, T) must be deterministic functions. Given the previously defined risk neutral dynamics of the short rate, we can insert the affine term structure expression in the general term structure PDE to obtain an affine pricing PDE and determine the following boundary conditions:
![]()
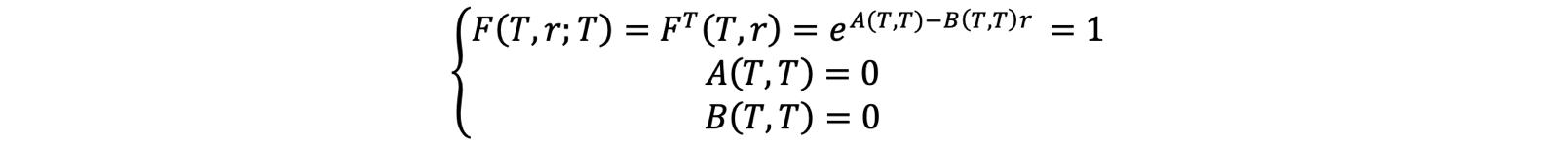
Note, if one requests ![]() and
and ![]() to be time independent,
to be time independent, ![]() and
and ![]() necessarily must be affine to allow the existence of an affine term structure (ATS). Thus, we assume:
necessarily must be affine to allow the existence of an affine term structure (ATS). Thus, we assume: ![]() and
and ![]() which leads to the affine PDE solution of [1]:
which leads to the affine PDE solution of [1]:
This equation holds for all t, T, and r. Therefore, let us consider it for a fixed choice of T and t. Since the equation holds for all values of r the coefficient of r must be equal to zero. We then obtain a Riccati equation for the determination of B which does not involve A, and which can be easily solved [1].
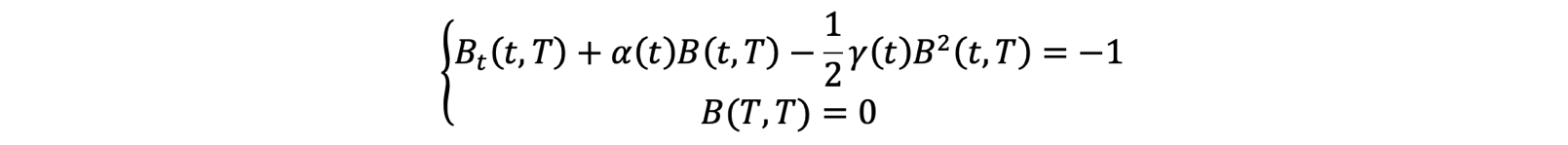
We then insert the solution for B from above into the expressions below and integrate to obtain A:
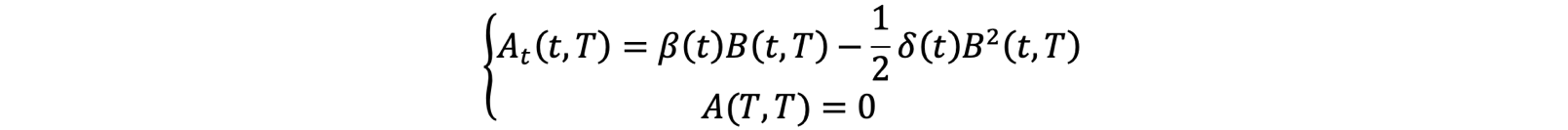
The advantage of an ATS model is that it allows for closed form pricing equations, requires no extensive numerical simulation and thus is computationally efficient and quick.
Vasicek Model:
The Vasicek model was one of the first short rate models. It specifies the Q dynamics of the short rate as:
![]()
It can be observed that the model entails a mean reversion component with a reversion level given by b/a and a speed of reversion parameter a. If the short rate is above its long-term mean, the model pushes it back down whilst if the rate is below the long-term mean, the model pushed the rate back up. This dynamic is quite a realistic assumption as it reflects the empirical rate behaviour across business cycles and the central bank’s reaction to them. The model assumes the following distributions: r(t) ~ Gaussian and I(t,T) ~ Gaussian where ![]() . The ATS equations then become [1]:
. The ATS equations then become [1]:
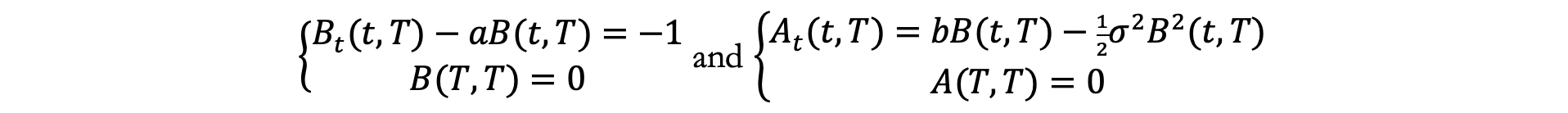
with the following solutions: ![]() and
and ![]() .
.
Next to the mean reversion dynamics, the main advantages of the model are that it allows for closed form pricing solutions and that it is simple to implement and calibrate to market data via minimising the squared error between market and model ZCB prices. On the other hand, disadvantages of the Vasicek model include that the discount factors are model based, the model allows for the possibility of negative rates due to its Gaussianity whilst also assuming perfect correlation among different rates along the maturity axis which is quite unrealistic. Also, as the mean and the volatility parameter are both time independent, the model only possesses a limited number of parameters to fit an infinite amount of asset prices in the continuous rates and volatility term structure, leading to an imperfect fit of the model term structure to the observed market term structure of rates and thus pricing errors. The current term structure of rates is an output rather than an input of the model which is why the Vasicek model can also be called an endogenous term-structure model. Additionally, given the lack of correlation modelling the model is unable to accurately price more complex derivatives like swaptions, caps and floors.
When calibrating the Vasicek model to empirical data, one tries to achieve the best possible fit to the observed market term structure. A simple calibration approach is thus to minimise the squared pricing error:
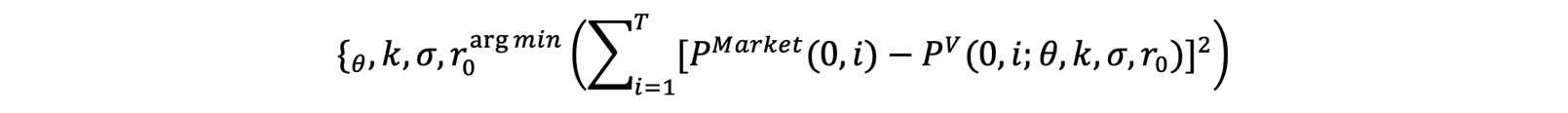 Even though in reality one can only observe a finite number of market bond prices, the limited number of parameters in the Vasicek model does not allow for a perfect term structure calibration.
Even though in reality one can only observe a finite number of market bond prices, the limited number of parameters in the Vasicek model does not allow for a perfect term structure calibration.
Note: ![]() can be estimated via maximum-likelihood-estimation using historical data. The MLE can then be used as a first guess for the true
can be estimated via maximum-likelihood-estimation using historical data. The MLE can then be used as a first guess for the true ![]() in the calibration process under Q. To derive the MLE for the Vasicek parameters, consider the historical measure model dynamics as having the form:
in the calibration process under Q. To derive the MLE for the Vasicek parameters, consider the historical measure model dynamics as having the form:
![]()
where ![]() is a parameter contributing to the market price of risk. Also assume that the market price of risk process
is a parameter contributing to the market price of risk. Also assume that the market price of risk process ![]() has the functional form
has the functional form ![]() in the short rate to obtain a short rate process that is tractable under both measures. This will help with the calibration (especially in the case when only very few prices are available in the market) since the diffusion coefficient is the same under the two measures and one can thus estimate from historical data through an MLE, while finding k and
in the short rate to obtain a short rate process that is tractable under both measures. This will help with the calibration (especially in the case when only very few prices are available in the market) since the diffusion coefficient is the same under the two measures and one can thus estimate from historical data through an MLE, while finding k and ![]() through calibration to market prices under Q. Suppose now that one can observe a series
through calibration to market prices under Q. Suppose now that one can observe a series ![]() of daily observations of a proxy of r(t) (for example a monthly rate, r(t) ≈ L(t, t + 1m)). The model parameters can then be estimated on the basis of this daily series of data [2]. Rewriting the historical dynamics as
of daily observations of a proxy of r(t) (for example a monthly rate, r(t) ≈ L(t, t + 1m)). The model parameters can then be estimated on the basis of this daily series of data [2]. Rewriting the historical dynamics as ![]() one can solve for
one can solve for ![]() by integration from any s to t:
by integration from any s to t:
![]()
and defining: , and note ![]() where
where ![]() is typically 1 day and denotes the time-step of the observed proxies
is typically 1 day and denotes the time-step of the observed proxies ![]() , one can derive the MLEs for
, one can derive the MLEs for ![]() as [2]:
as [2]:
![]() ,
,
![]() ,
,
![]()
The estimated quantities give complete information on the ![]() -transition probability for the process r under the historical measure. Thus, one can simulate at one-day spaced future discrete time instants to determine
-transition probability for the process r under the historical measure. Thus, one can simulate at one-day spaced future discrete time instants to determine ![]() and then estimate the remaining parameters required for risk-neutral pricing as usual by calibration to market prices under Q.
and then estimate the remaining parameters required for risk-neutral pricing as usual by calibration to market prices under Q.
Vasicek Pricing Solutions:
Let us now discuss some Vasicek solutions to pricing. When pricing a bond option on a ZCB with exercise date T, bond maturity S, strike X, Gaussian CDF ![]() we get:
we get:
![Rendered by QuickLaTeX.com BondOpt\left(t,T,S,X\right)=E_t^Q\left[{e^{-\int_{t}^{T}r\left(s\right)ds}\ast w(P\left(T,S\right)-X)}^+\right] ={P(t,T)E}_t^T\left[{w(P\left(T,S\right)-X)}^+\right]=w[P\left(t,S\right)\mathrm{\Phi}\left(wh\right)-X\ast P\left(t,T\right)\mathrm{\Phi}\left(w(h-\sigma_P\right))]](https://bsic.it/wp-content/ql-cache/quicklatex.com-c10e734b6585870785f6e6926d48b4e4_l3.png)
with ![]() and
and ![]() with w = 1 for calls and w = -1 for puts. Note, the pricing is initially done under the risk neutral measure Q before switching to the T-forward measure
with w = 1 for calls and w = -1 for puts. Note, the pricing is initially done under the risk neutral measure Q before switching to the T-forward measure ![]() with the T-bond numeraire as this greatly simplifies the calculations (the change of measure will be briefly discussed below). The specifications under the T-forward measure
with the T-bond numeraire as this greatly simplifies the calculations (the change of measure will be briefly discussed below). The specifications under the T-forward measure ![]() can be described as [2]:
can be described as [2]:
Short rate dynamics:
![]()
With ![]() -Brownian motion
-Brownian motion ![]() :
:
![]()
So that for s≤t≤T:
![]()
With: 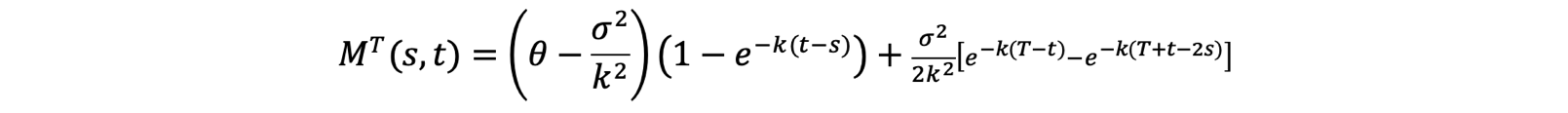
Intuition behind the change of measure:
When dealing with the pricing of interest rate derivatives, the change of measure (also known as the change of numeraire) is often applied as this trick allows to greatly simplify calculations. The reasoning behind this is the following: Using the usual money market account as a numeraire can be problematic in our applications as when interest rates are stochastic in order to use the formula ![]() , one needs to know the joint distribution of
, one needs to know the joint distribution of ![]() and
and ![]() . This is not easy as the two quantities are not independent under the normal risk neutral measure. It is more convenient to reformulate the pricing problem using as the new numeraire the traded ZCB with maturity
. This is not easy as the two quantities are not independent under the normal risk neutral measure. It is more convenient to reformulate the pricing problem using as the new numeraire the traded ZCB with maturity ![]() especially when pricing derivatives which contain the expectation of forward bond prices in their pricing equation e.g. bond options. It follows:
especially when pricing derivatives which contain the expectation of forward bond prices in their pricing equation e.g. bond options. It follows:
![]()
The associated probability measure is called T-forward measure as under it the forward price v(t)/P(t,T) is a martingale:
![]()
Note: The forward rate ![]() is only a martingale under the forward measure
is only a martingale under the forward measure ![]() . Each forward rate with a different maturity is a martingale under its own particular measure. To price more complex derivatives, one needs to jointly model rates of different maturities under a single pricing measure. Thus to rewrite the forward rate processes under the same measure, one needs a change of measure via Girsanov‘s theorem, which introduces drift terms to all processes whose forward measure is not taken as the pricing measure. It can be shown by no arbitrage, that the instantaneous forward rate f(t,T) is also a martingale under the forward measure. Also note: The expectation hypothesis
. Each forward rate with a different maturity is a martingale under its own particular measure. To price more complex derivatives, one needs to jointly model rates of different maturities under a single pricing measure. Thus to rewrite the forward rate processes under the same measure, one needs a change of measure via Girsanov‘s theorem, which introduces drift terms to all processes whose forward measure is not taken as the pricing measure. It can be shown by no arbitrage, that the instantaneous forward rate f(t,T) is also a martingale under the forward measure. Also note: The expectation hypothesis ![]() is only true under the forward measure and does not hold under the normal risk neutral measure Q. Under the forward measure the present forward rate is an unbiased estimator of the future spot rate.
is only true under the forward measure and does not hold under the normal risk neutral measure Q. Under the forward measure the present forward rate is an unbiased estimator of the future spot rate.
Vasicek Derivative Pricing continued:
With this in mind, now let us take a look at the Vasicek closed form pricing solution for caplets considering a caplet on the simple Libor rate with exercise date T, maturity S, strike K, Gaussian CDF ![]() :
:
 The result is convenient as the Vasicek model allows to price caplets as a function of ZCB bond option prices. To obtain the final prices of Caps one then only needs to sum up the prices of the individual Caplets included in the Cap. Note: The pricing is initially demonstrated here under the Q measure exploiting the tower property of expectations, before switching to the T-forward measure with the T-bond numeraire to obtain the final result. As mentioned before, one drawback of the Vasicek model is that the model is unable to perfectly fit the volatility term structure quoted in the market. Given its relevance for cap pricing, the Vasicek model leads to pricing inaccuracies when applied to caplets, floorlets and swaptions.
The result is convenient as the Vasicek model allows to price caplets as a function of ZCB bond option prices. To obtain the final prices of Caps one then only needs to sum up the prices of the individual Caplets included in the Cap. Note: The pricing is initially demonstrated here under the Q measure exploiting the tower property of expectations, before switching to the T-forward measure with the T-bond numeraire to obtain the final result. As mentioned before, one drawback of the Vasicek model is that the model is unable to perfectly fit the volatility term structure quoted in the market. Given its relevance for cap pricing, the Vasicek model leads to pricing inaccuracies when applied to caplets, floorlets and swaptions.
Alternative approach to ZCB pricing for Gaussian models:
Instead of using the ATS PDE approach, ZCB prices for Gaussian models can also be found via the characteristic function of Gaussian random variables: ![]() Given r(t) is Gaussian under Vasicek, also its integral
Given r(t) is Gaussian under Vasicek, also its integral ![]() is Gaussian with:
is Gaussian with: ![Rendered by QuickLaTeX.com E\left[\int_{t}^{T}r\left(s\right)ds\right]={\frac{r_t-\theta}{k}\left(1-e^{-k\left(T-t\right)}\right)-}\theta(T-t),Var\left[\int_{t}^{T}r\left(s\right)ds\right]=\frac{\sigma^2}{{2k}^3}(2k\left(T-t\right)-3+4e^{-k\left(T-t\right)}-e^{-k2\left(T-t\right)}](https://bsic.it/wp-content/ql-cache/quicklatex.com-6095beb1d03b4a61860d3b5be03dbc55_l3.png) which then allows to apply the characteristic function mentioned above as remember
which then allows to apply the characteristic function mentioned above as remember ![]()
Cox-Ingersoll-Ross Model (CIR):
To solve some of the issues of the Gaussian Vasicek model, Cox, Ingersoll and Ross developed an ATS model which entails a square root term of the short rate, thus forcing the rate to be positive whilst keeping the mean reversion mechanism. The CIR model dynamics are given ![]() with ATS solutions:
with ATS solutions:

where ![]() [1]. Given the structure, the rate is now no longer distributed as a Gaussian random variable but instead follows a non-central chi-squared distribution. To grant that the rate remains always positive, one needs to impose
[1]. Given the structure, the rate is now no longer distributed as a Gaussian random variable but instead follows a non-central chi-squared distribution. To grant that the rate remains always positive, one needs to impose ![]() so that when rate r goes to 0, the drift term dominates pushing the rate upwards. However, given the recent history of negative rates, it can be debated whether this model feature is desirable or not. Just like in the Vasicek model, the CIR allows for closed form pricing solutions, considers rate mean reversion and has model based discound factors. Thus, the CIR model is also unable to perfectly calibrate to the observed market term structures as well as to realistically model correlation dynamics, leading to pricing errors.
so that when rate r goes to 0, the drift term dominates pushing the rate upwards. However, given the recent history of negative rates, it can be debated whether this model feature is desirable or not. Just like in the Vasicek model, the CIR allows for closed form pricing solutions, considers rate mean reversion and has model based discound factors. Thus, the CIR model is also unable to perfectly calibrate to the observed market term structures as well as to realistically model correlation dynamics, leading to pricing errors.
To price a bond option using the CIR model, let us rewrite the model as: ![]() . The t price of a European call option on an underlying bond with maturity S with strike K and exercise date T is then given by [2]:
. The t price of a European call option on an underlying bond with maturity S with strike K and exercise date T is then given by [2]:
![Rendered by QuickLaTeX.com c\left(t,T,S,K\right)=P\left(t,S\right)\ast\mathcal{X}^2\left(2r^\ast\left[\phi+\psi+B\left(T,S\right)\right];{\frac{4k\theta}{\sigma^2}\ ,\ \ \ {\frac{2\phi^2r_te^{h\left(T-t\right)}}{\phi+\psi+B\left(T,S\right)}}}\right)-KP(t,T)\mathcal{X}^2\left(2r^\ast\left[\phi+\psi\right];{\frac{4k\theta}{\sigma^2}\ ,\ \ \ {\frac{2\phi^2r_te^{h\left(T-t\right)}}{\phi+\psi}}}\right)](https://bsic.it/wp-content/ql-cache/quicklatex.com-a0fe7094397d53e336850576fbc053ed_l3.png)
where:
![]()
![]()
![]()
![]()
Note: ![]() is a non-central chi-squared distribution function with
is a non-central chi-squared distribution function with ![]() degress of freedom and non-centrality parameter
degress of freedom and non-centrality parameter ![]()
Ho-Lee model:
Having discussed two models with time-independent parameters, let us now turn to the Ho-Lee model – one of the first models with partially time dependent parametrization. Specifically, the Ho-Lee model expresses the short rate dynamics as ![]() where r(t) and its integral follow Gaussian distributions [1]. The ATS equations then become:
where r(t) and its integral follow Gaussian distributions [1]. The ATS equations then become:
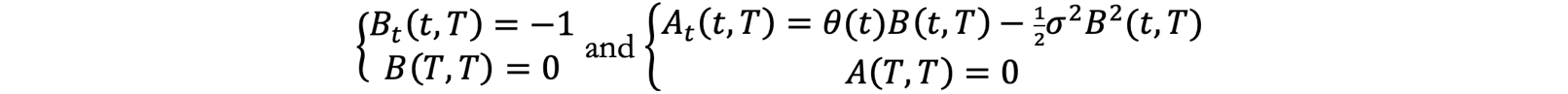
with solutions ![]() and
and ![]() Most importantly,
Most importantly, ![]() is now allowed to vary dynamically over time leading to the model possessing an infinite number of parameters which in turn allows to perfectly calibrate the resulting Ho-Lee term structure to the market observed term structure. In detail, one determines
is now allowed to vary dynamically over time leading to the model possessing an infinite number of parameters which in turn allows to perfectly calibrate the resulting Ho-Lee term structure to the market observed term structure. In detail, one determines ![]() to fit the market term structure {p*(0,T);T≥0} by setting p(0,T)=p*(0,T) with solution:
to fit the market term structure {p*(0,T);T≥0} by setting p(0,T)=p*(0,T) with solution: ![]() , where
, where ![]() are the forward rates quoted by the market. Thus, Ho-Lee is the first model we present that allows for closed form pricing solutions whilst using perfectly calibrated market-based discount factors. However, given its simplistic drift term, the model does omit the mean reversion characteristics of the previous models and given its Gaussianity also allows for the possibility of negative rates. Additionally, the model still assumes perfect correlation among rates which again leads to pricing inaccuracies when applying the model to more complex derivatives such as swaptions.
are the forward rates quoted by the market. Thus, Ho-Lee is the first model we present that allows for closed form pricing solutions whilst using perfectly calibrated market-based discount factors. However, given its simplistic drift term, the model does omit the mean reversion characteristics of the previous models and given its Gaussianity also allows for the possibility of negative rates. Additionally, the model still assumes perfect correlation among rates which again leads to pricing inaccuracies when applying the model to more complex derivatives such as swaptions.
Having calibrated it to the market, the Ho-Lee term structure and thus Ho-Lee ZCB prices are given by:
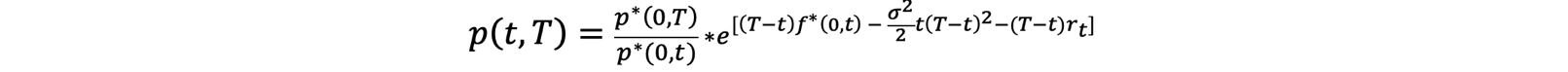
The t price of a European call option on an underlying ZCB with maturity S with strike K and exercise date T is given by:
![]()
![]()
Hull-White 1 Factor Model:
The Hull-White 1 Factor model was the first model which tried to combine the advantages of the Vasicek and Ho-Lee models by combining a time-varying drift term and mean reversion. The model dynamics are given by:
where r(t) once again follows a Gaussian distribution [1]. The ATS equations become:
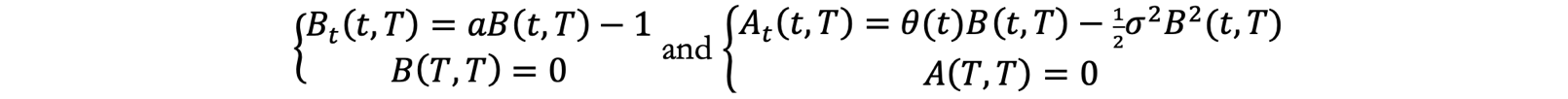
with solutions ![]() and
and ![]() Note: In an affine model, the forward rates are given by
Note: In an affine model, the forward rates are given by ![]() . The function
. The function ![]() is then chosen matching the model with the market quoted forward rates, thus the one solving:
is then chosen matching the model with the market quoted forward rates, thus the one solving:
![]()
The Hull-White model has a perfect fit to the market term structure as it extends the Vasicek model via a deterministic function g(t) which if properly parameterised can adapt to all term structure shapes which can be shown by writing:
![]()
Now plug in the rate dynamics of the Vasicek model ![]() for
for ![]()
![]() and replace
and replace ![]() with
with ![]() as defined above:
as defined above:
![]()
Finally, collect the terms:
![Rendered by QuickLaTeX.com =k\left(\left[\underbrace{{\frac{g\prime(t)}{k}+\theta+g(t)}}\right]-r^{HW}\left(t\right)\right)dt+\sigma dW_t](https://bsic.it/wp-content/ql-cache/quicklatex.com-fa8c8d50413971f830ba21c1ad42877a_l3.png)
resulting in the Hull-White 1 factor model:
![]()
The previous results can be used to simplify the calibration of the Hull-White model to the market term structure. This can be shown by considering:
![]()
The expectation term now equals the known Vasicek ZCB price leading to:
![]()
If one assumes the deterministic g(t) to be piecewise constant, one can achieve an exact term structure calibration via bootstrapping.
To calibrate the model to the market set:
![]()
Via piecewise constant assumption one then gets:
![]()
And as the market price and the Vasicek price are known, one can now solve for the function and bootstrap:
For 0≤T<1y: ![]()
Then we solve for the value of the function: ![]() and use the result to bootstrap for longer periods: For 1≤T<2y:
and use the result to bootstrap for longer periods: For 1≤T<2y: ![]()
Here ![]() and
and ![]() are known, so one can solve for
are known, so one can solve for ![]() and continue bootstrapping to calibrate the entire term structure.
and continue bootstrapping to calibrate the entire term structure.
Having calibrated it to the market, the Hull-Wite 1 Factor term structure and thus HW1 ZCB prices are given by:
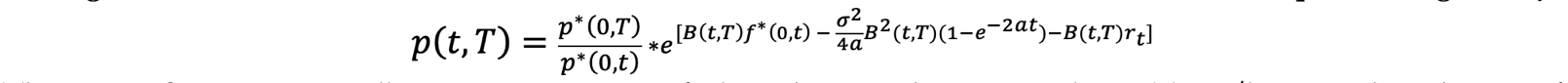
The price of a European call option at t on an underlying ZCB with maturity ![]() with strike K and exercise date
with strike K and exercise date ![]() is given by:
is given by:

Note: ![]() represents the integrated instantaneous variance. Analogously, the price of a European put option zbp(
represents the integrated instantaneous variance. Analogously, the price of a European put option zbp(![]() ) can be computed as:
) can be computed as:
![]()
Given the formulas for ZCB call and put options, one can also price caps and floors since they can be viewed as portfolios of zero-bond options. To do so, denote by ![]() the set of the cap/floor payment dates and by
the set of the cap/floor payment dates and by ![]() the set of the corresponding times, meaning that
the set of the corresponding times, meaning that ![]() is the difference in years between
is the difference in years between ![]() and the settlement date t, and where
and the settlement date t, and where ![]() is the first reset time. Also, denote by
is the first reset time. Also, denote by ![]() the year fraction from
the year fraction from ![]() for i = 1, …, n. One then obtains the price at time
for i = 1, …, n. One then obtains the price at time ![]() of the cap with cap rate (strike) X, nominal value N and set of times
of the cap with cap rate (strike) X, nominal value N and set of times ![]() as [2]:
as [2]:
![]()
with:

![]()
and the corresponding price of a floor:
![]()
So far, we have only considered options on zero coupon bonds, but one can also derive explicit solutions for the prices of European options on coupon-bearing bonds under Hull-White dynamics. For this, consider a European option with strike X and maturity T, written on a bond paying n coupons after the option maturity. Denote by ![]() , and by
, and by ![]() the payment time and value of the i-th cash flow after T. Let
the payment time and value of the i-th cash flow after T. Let
![]() . Denote by r* the value of the spot rate at time T for which the coupon-bearing bond price equals the strike and by X the time-T value of a pure-discount bond maturing at T when the spot rate is r*. Then the option price at time t < T is [2]:
. Denote by r* the value of the spot rate at time T for which the coupon-bearing bond price equals the strike and by X the time-T value of a pure-discount bond maturing at T when the spot rate is r*. Then the option price at time t < T is [2]:
![]()
where CBO stands for an option on a coupon bearing bond and ZBO for an option on a ZCB. Note: Given this analytical formula, also European swaptions can be analytically priced, since a European swaption can be viewed as an option on a coupon-bearing bond [2].
To do so, consider a payer swaption with strike rate X, maturity T and nominal value N, which gives the holder the right to enter at time an interest rate swap with payment times: ![]() , where she pays at the fixed rate X and receives LIBOR set “in arrears”. Denote by the year fraction from to , i = 1,…,n and set := for i = 1,…,n−1 and := . Denoting by the value of the spot rate at time T for which:
, where she pays at the fixed rate X and receives LIBOR set “in arrears”. Denote by the year fraction from to , i = 1,…,n and set := for i = 1,…,n−1 and := . Denoting by the value of the spot rate at time T for which:
![]()
where: 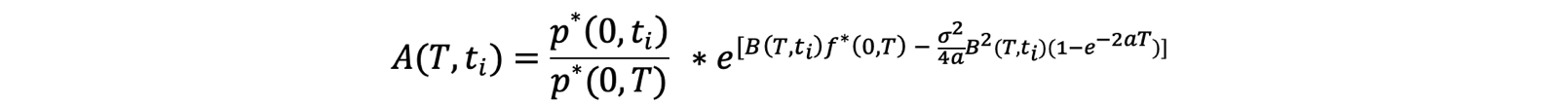
and setting:
![]()
then the payer swaption price at t<T is given by:
![]()
and the receiver swaption price at t<T is given by:
![]()
where ZBP denotes a European put option on a ZCB and ZBC a European call option on a ZCB [2].
In its simple 1 factor form, the Hull-White model is still assuming a constant diffusion parameter and perfect correlation between rates which does not allow it to calibrate well to the volatility term structure observed in the market or to price correlation sensitive derivatives without major pricing errors. With this in mind, let us know discuss two possible extensions of the standard Hull-White model to offer potential remedies to these issues.
Hull-White Model Extension A: Time-Varying Volatility
The initial HW model can be extended to include a time-varying volatility parameter so that the Q dynamics become:
![]()
One advantage of this extension is that the model can now be perfectly fitted to the term structure of interest rates and the term structure of spot or forward-rate volatilities. However, the perfect fitting to a volatility term structure can be rather dangerous and must be carefully dealt with for two reasons. First, market activity tends to cluster around certain volatilities and not all volatilities quoted in the market are significant. Some market segments are less liquid than others implying that the associated quotes becoming neither informative nor reliable. Second, the model is likely to imply unrealistic future volatility structures as they tend to differ from the “humped“ volatility shapes typically observed in the market [2]. Given these disadvantages, this particular extension of the model is rarely used.
Hull-White Model Extension B: Two-Factor Model
The second extension is more relevant and improves the original HW model by introducing a second risk factor with an associated correlation structure. The model dynamics thus become:
![]()
![]()
![]()
As can be easily seen, the extension allows to model an imperfect correlation structure between the two factors implying that the long and short end of the curve can now be modelled separately which in turn improves pricing compared to other models. As an intuitive interpretation of the two factors, one could say that the first factor controls the levels of the rates whilst factor 2 controls the steepness of the forward curve. The correlation coefficient between the two risk factors is typically a large negative number reflecting the fact that a steepening curve tends to correlate negatively with parallel rate shifts. However, given its static diffusion parameter, even the two factor Hull-White model is still unable to accurately fit the market quoted volatility term structure. For this purpose, it is recommendable to instead use models like the SABR. Also, whilst the second factor improves pricing performance, two factors are still not sufficient to accurately price sophisticated derivatives like Bermudan swaptions. For these purposes, it would be advisable to use models which directly model individual forward rates to minimise pricing errors such as the Brace Gatarek Musiela (BGM, also known as Libor Market Model).
Conclusion
Throughout this primer, we have identified several advantages of using affine term structure (ATS) models. Beyond their computational efficiency, these models offer closed-form pricing solutions. For models with time-dependent parameters, optimal calibration to the market term structure can be achieved. Additionally, all the short-rate models discussed can be approximated using lattice methods, enabling the pricing of early-exercise derivatives. Pricing can be further simplified by applying the change-of-measure techniques.
However, we have also recognized certain weaknesses in these models. Most notably, models with time-independent parameters fail to perfectly fit the market term structure, leading to pricing errors. With the exception of the first Hull-White extension, all the models presented exhibit limitations in modelling correlations and fitting the market volatility term structure, which results in additional pricing errors, particularly for complex derivatives such as Bermudian swaptions. Furthermore, Gaussian models allow interest rates to become negative—though lower bounds can be introduced to mitigate this issue—while the CIR model imposes a strict non-negativity constraint, which may be unrealistic in periods of unconventional monetary policy.
Despite these limitations, short-rate models remain a crucial foundation in the evolution of interest rate modelling, serving as a bridge to more advanced frameworks such as the Heath-Jarrow-Morton (HJM) and Brace-Gatarek-Musiela (BGM) models.
References
[1] Björk, T. “Arbitrage Theory in Continuous Time”, ed. 4, 2019.
[2] Brigo, D. & Mercurio, F. “Interest Rate Models – Theory and Practice: With Smile, Inflatio and Credit”, 2006.
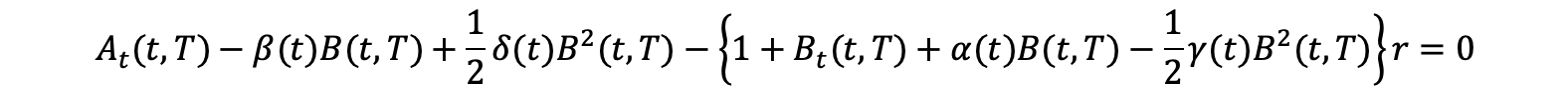



0 Comments