Building a poker bot: Game theory and Neural networks

Download PDF

Note that this is an academic project and we have no intention to utilize this project in real cash online poker as that goes against services terms of conditions.

It is no coincidence that poker is frequently mentioned when discussing the world of trading, and that even firms like Susquehanna International Group use poker to sharpen their trading-skills. In both domains, success depends not just on raw calculation but on managing risk, reading signals, exploiting patterns, and balancing aggression with caution. Building a poker bot is a challenging task that blends game theory, probability, and computer science. What makes a project like this even more intriguing is that, unlike classic games such as chess, poker is a game of imperfect information where players have hidden cards, and outcomes involve chance. This article explores the game theory that underpins poker, the challenges posed by imperfect information, and how these ideas translate into building an intelligent poker bot.

Imperfect Information games

To build a poker bot, we must first understand the environment of poker itself. In a perfect information game, all players always have full knowledge of the game state. In contrast, poker is an imperfect information game: each player has private information (their hole cards) that others cannot see. This means the true “state” of the game is not clearly defined from any one player’s perspective; thus, you never know exactly what situation you are in. Instead, you must consider a distribution of possible states consistent with the information you do have. In formal terms, poker is represented as an extensive-form game with imperfect information, where a player’s decision point corresponds to an information set: a set of different histories (dealings of cards and actions) that are indistinguishable to that player. The player must devise a strategy that works well against all possibilities in that info set. In short, you are always making decisions under uncertainty. 

One consequence of hidden information is that probabilistic strategies and deception become crucial. Whereas a perfect-information game might have a clearly defined best move in each situation, an imperfect-information game often has no single best move: the optimal play might be to randomize. A classic toy example is Rock-Paper-Scissors. This simple game (often cited in game theory) has no dominant pure strategy; any fixed action can be exploited by an opponent who guesses it. The solution is a mixed strategy: throw each of rock, paper, scissors with 1/3 probability, which is a Nash equilibrium. The need for such randomization in Rock-Paper-Scissors illustrates how optimal play in imperfect information games typically involves mixing actions, keeping opponents indifferent and unable to exploit patterns. Poker shares this property: a strong poker strategy will sometimes bet with weak hands and check with strong hands, in just the right frequencies, to avoid giving away information or being exploited.

Counterfactual Regret Minimization

Counterfactual Regret Minimization, or CFR for short, is the most crucial part to understanding modern poker bots. CFR is an iterative algorithm that finds approximate Nash equilibrium strategies by applying the concept of regret minimization to decision points in an extensive-form game. It was first introduced by Martin Zinkevich and colleagues in 2007 and has since formed the basis of many breakthrough poker AIs. Intuitively, CFR works by having the two players play against each other repeatedly in simulation, gradually adjusting their strategies to eliminate regret. Regret, in this context, means looking back and asking: “If I had chosen a different action in a given situation, would I have achieved a better outcome on average?” If the answer is yes, then the player has positive regret for not having taken that action. CFR’s update rule will then increase the probability of that action in the strategy for the next iteration. Conversely, actions that would have done worse get their probabilities reduced. Over millions of iterations, these regret updates probably lead the strategy to converge toward a Nash equilibrium, where no action has positive regret (meaning no single deviation would have improved the outcome). At convergence, the average strategy of the iterations is essentially GTO. 

In two-player zero-sum games like poker, CFR guarantees that if both players minimize regret, the resulting strategy profile approaches an equilibrium. A key innovation of CFR is focusing on counterfactual regret at each information set (each decision situation a player can face), rather than overall outcomes. In each iteration of self-play, CFR traverses the game tree and computes payoffs as if one player had fixed their strategy and the other tries different actions. The algorithm determines how much immediate counterfactual regret each action has, roughly “how much better could you have done in this info-set if you had chosen action A instead of your current strategy?”. These regrets are accumulated over iterations. Then regret matching is applied: the strategy is updated so that the probability of each action is proportional to the positive cumulative regret of not having played that action in the past. Intuitively, if an action has caused a lot of regret (it would have often improved outcomes had it been played more), then the algorithm will choose that action more frequently going forward. CFR applies this regret update at every decision point (for both players) on each iteration. Remarkably, it can be shown that if this process continues indefinitely, the average strategy converges to a point where regrets are zero: a Nash equilibrium. In practice, CFR converges within tolerable error after a finite (but possibly very large) number of iterations. One iteration of CFR essentially consists of a full traversal of the game tree to compute regrets, followed by a strategy update. (This is a huge problem for us if we want to build a poker bot, and how we handle this is explained in depth later in the article.)

To better understand CFR, we turn back to the example of Rock Paper Scissors, a “toy game” in our case of applying CFR to Poker. As we all know, in this game, there are two players, each selecting either Rock, Paper, or Scissors. A win gives +1, a loss gives −1, and a tie gives 0. The payoff table for RPS is as follows:

If one has studied basic Game Theory, a Nash equilibrium, if being a one-shot game, does not exist. Although, suppose we play Rock, and our opponent also plays Rock. Both players receive a reward of 0 (a tie). Now, CFR asks: “What if I had chosen differently?” Our counterfactual rewards are the payoffs we would have received if we had taken each other’s possible action instead.

• If we had chosen Scissors, we would have lost (−1).
• If we had chosen Paper, we would have won (+1).

These regrets are stored and accumulated over many iterations. In the next round, suppose we again choose Rock, but the opponent plays Paper. Our actual reward is −1. The counterfactual rewards would be:

• Rock: −1
• Paper: 0 (tie)
• Scissors: +1 (win)

The regrets this round are:

We then add these regrets to the running totals from previous rounds. For example, if Scissors had −1 regret before and now has +2, the total becomes +1. This accumulation is crucial: we don’t just look at one round, we learn over time by summing all regrets.

We now want to minimize future regret by playing proportionally more of the actions with higher positive regret. We do this by normalizing the positive regrets to form a probability distribution:

When two CFR players train against each other, each updating their strategy by minimizing regret, their average strategies will converge to a Nash equilibrium. In Rock Paper Scissors, the Nash equilibrium is the completely mixed strategy:

At equilibrium, neither player can improve their long-term expected payoff by deviating. In practice, this equilibrium emerges after thousands of iterations of self-play, where each player continually updates based on accumulated regrets.

Over time, researchers have developed several variants of CFR to improve its efficiency and scalability. The original Vanilla CFR algorithm traverses the entire game tree in every iteration, updating regrets for each information set. While this guarantees reliable convergence, it is computationally infeasible for large games like Texas Hold’em, which contains on the order of 3*1014 decision points. As a result, Vanilla CFR is mainly used for smaller abstracted games or theoretical analysis. To address this limitation, Monte Carlo CFR (MCCFR) was introduced as a family of sampling-based methods. Instead of exploring every possible path in the game on each iteration, MCCFR randomly samples specific trajectories, such as card deals or action sequences and updates regrets only along those sampled paths. Over many iterations, this stochastic approach approximates the same result as full CFR in expectation, while drastically reducing computational requirements. Although MCCFR introduces some variance into the updates, its efficiency gains make it possible to compute near-equilibrium strategies in games that are otherwise too large for exact CFR, marking a major step forward in practical poker AI.

Abstractions

As briefly mentioned before, one major hurdle remains: Texas Hold’em is an astronomically large game. Even with efficient algorithms like MCCFR, solving the full game without simplification is beyond current computational limits, especially true for No-Limit Hold’em, which has a huge range of possible bet sizes. To make the problem tractable, poker AI researchers employ abstractions: simplified versions of the game that are small enough to solve, yet hopefully close enough to the real game that the solution is still strong. Abstraction is essentially a form of lossy compression of the game’s state space or action space. 

The most common form of information abstraction in poker is card abstraction, also known as hand bucketing. The idea is to partition the many possible private hand combinations (and public card combinations) into a smaller number of buckets or categories, treating all hands in the same bucket as identical for the strategy. For example, pre-flop in Hold’em there are 52 choose 2, i.e. 1,326 distinct hole card combinations. Many of these are very similar in value, for example K♥Q♣ and K♦Q♠ are essentially the same. A classic abstraction is to group hands by their rank structure and suits, yielding 169 canonical pre-flop hands. In this scheme, all suited vs unsuited versions are merged. This drastically cuts down the state space at the very start. Similarly, post-flop, there are thousands of possible card combinations of board + hand, which can be grouped by strength. Early research and bots often used a hand strength heuristic for bucketing: for instance, use the hand’s equity (expected win probability) as a key metric.

In poker, equity is a measure of how strong a hand is relative to random opposition. Formally, a hand’s equity can be defined as the probability that the hand would win at showdown (plus half the probability of tying) against a random hand, given a uniform random distribution of future community cards. This is also called expected hand strength (EHS). We can calculate equity by enumerating or Monte Carlo simulating all possible outcomes. A simple abstraction might be to group hands into buckets by ranges of equity. One quoted approach was to use 10 buckets preflop, 100 on the flop, 1000 on the turn, 10,000 on the river, essentially an exponentially growing number of buckets each round to capture the increasing complexity as more cards are revealed.

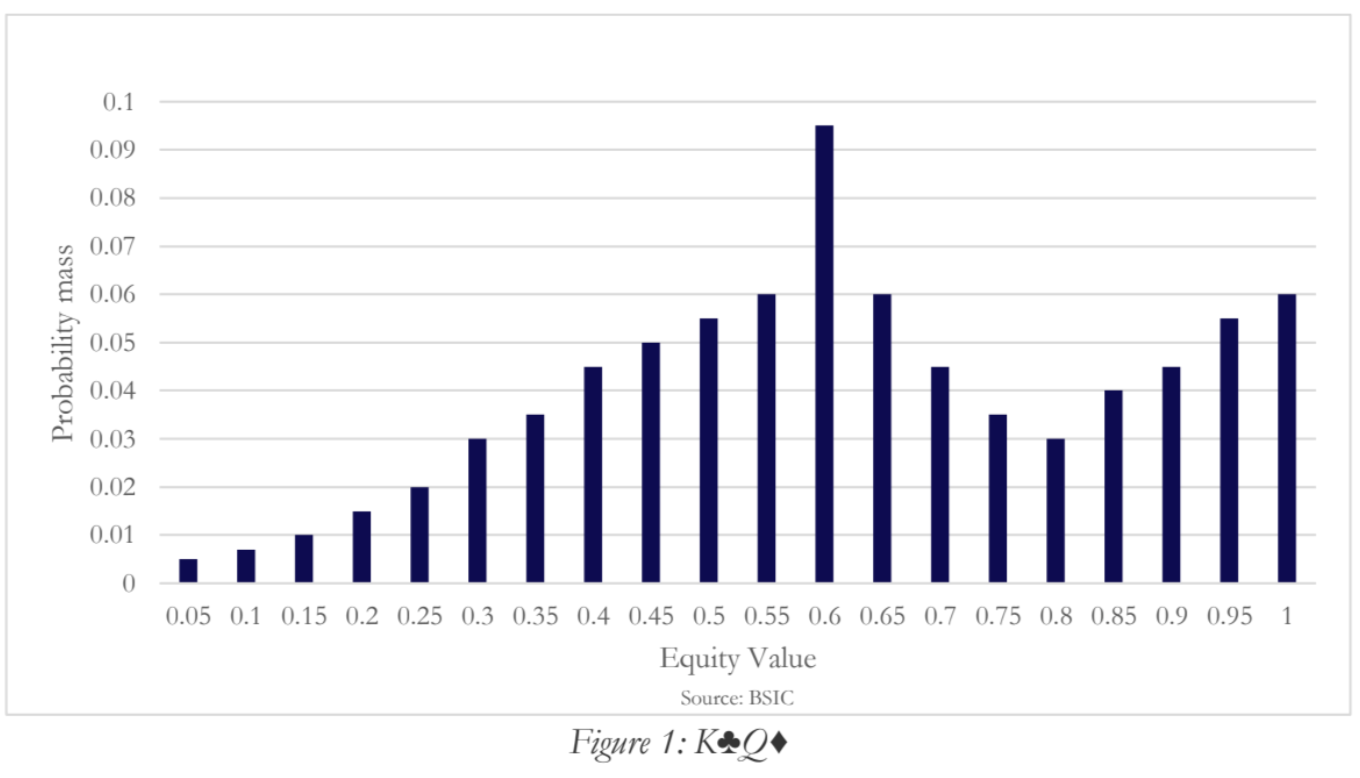
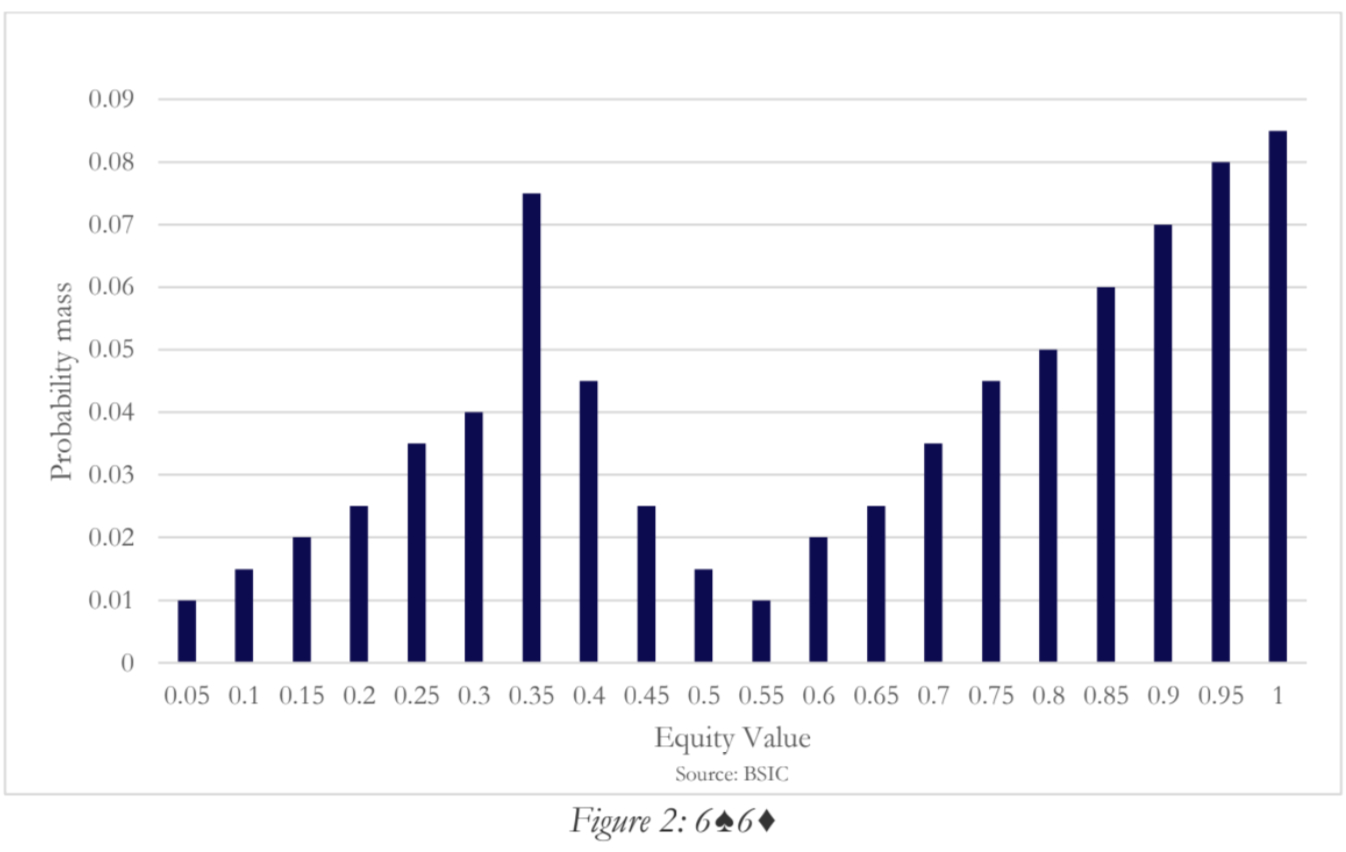
However, a major problem was discovered with naive equity-based bucketing: hands that have similar overall equity can play very differently. Equity alone “doesn’t paint the entire picture”. For example, consider two hands like 6♠6♦ and K♣Q♦. Preflop, both might have roughly 64% equity versus a random hand. If we bucket purely by equity, 66 and KQ could end up grouped together. But any poker player knows 66 and KQ are strategically quite different. The solution developed by researchers is to use distributional information: not just a single equity value, but the entire equity distribution of a hand across future possibilities. This led to what’s called distribution-base abstraction. Concretely, instead of representing a hand by one number (its average win rate), we represent it by a histogram of outcomes. For each hand and board situation, we can simulate all possible ways the remaining cards could be dealt and record the hand’s equity in each scenario. This yields a distribution (for example, hand X might win 0% in 30% of outcomes, 50% in 20% of outcomes, 100% in 50% of outcomes, etc.). We then cluster these distributions: two hands that have similar shapes to their equity histogram are grouped together. This is done by employing k-means clustering on these equity vectors, using a distance metric like Earth Mover’s Distance (EMD) to compare distributions. 

Demo poker bot

To test the theory in real life, we attempted to build our own poker neural network bot to advise us on the best possible play based on the actual game situation. This bot does not just consider the mathematical strength of your cards and theoretical structures such as game theory; it also uses its ‘experience’ to evaluate which plays have worked best in the past. It gains this experience through training. This training involves reviewing thousands of real-life games with real hands. By working with this data, the bot identifies patterns and strategies and analyses their success rate. The more the bot is trained, the more accurate its advice becomes.

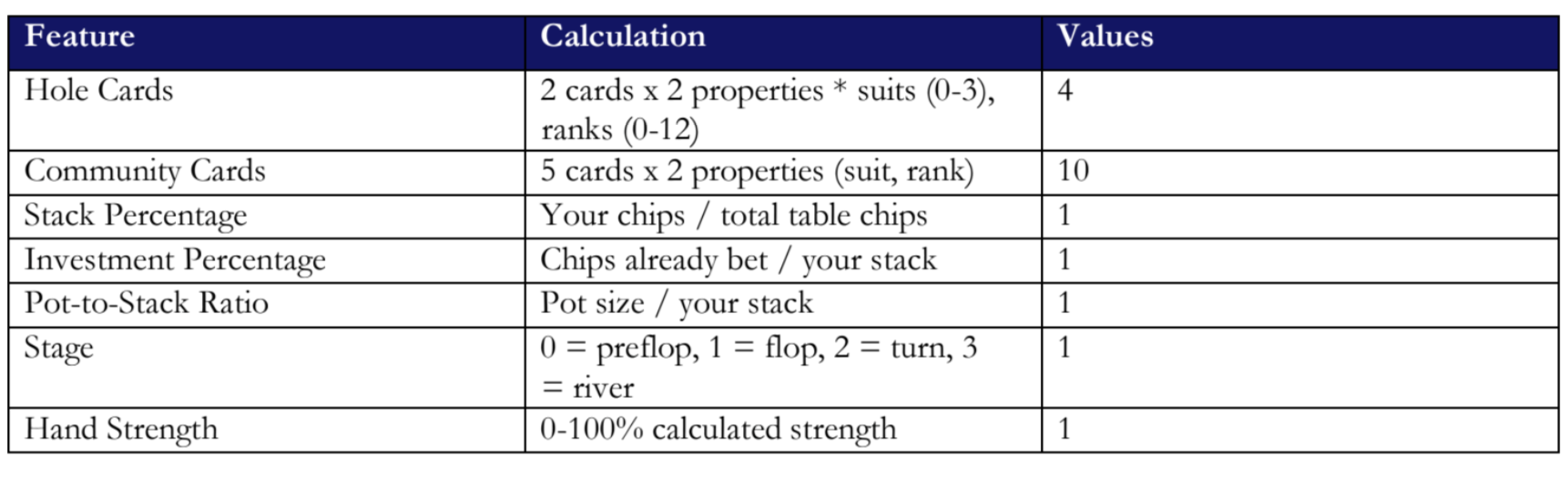
Firstly, the user must enter the current stage of the game. This includes the given two hole cards, the community cards (0–5, depending on the stage), your position, your chip stack, the total chips at the table, the chips you have bet this hand, the current pot size, the amount to call, the big blind, the small blind, the number of active players, and the stage. After inserting this information, the bot translates it into values. The following table shows how these values are created:

These values then undergo different layers of analysis by different neurons, whereby the bot attempts to recognize patterns and complex strategies with a high probability of success. A neuron can therefore be thought of as a tiny memory of the bot from its training. This could be the simple recognition of a situation, such as ‘high pocket pair’, or it could be the connection of different recognitions resulting in a specific possible action, such as ‘weak hand + small pot + early stage = safe to see more cards’. The layers represent ‘filter stages’. As the user moves forward through the layers, the inputs are analyzed for more complex patterns and strategies, which is why the number of neurons decreases. This enables the bot to focus its analysis and consider possible actions in more depth, ultimately determining the most successful play. In practice, the first layer contains 128 neurons that detect basic poker patterns, such as ‘low chip stack’, for example. If the detected patterns are strong, a high value is given as an output. If the patterns detected are weak or absent, the bot stays quiet (i.e. it doesn’t provide an output). The bot then moves on to the second layer, which has 64 neurons. During this stage, simple patterns are combined to form more complex poker concepts. The third layer has 32 neurons for detection. Here, poker concepts are converted into strategic decisions such as ‘apply pressure with a raise’. The data then arrives at the final layer, layer four. This layer has three neurons representing the probability of folding, calling/checking, and raising/betting. Based on these probabilities the bot makes a final decision on which action to take.

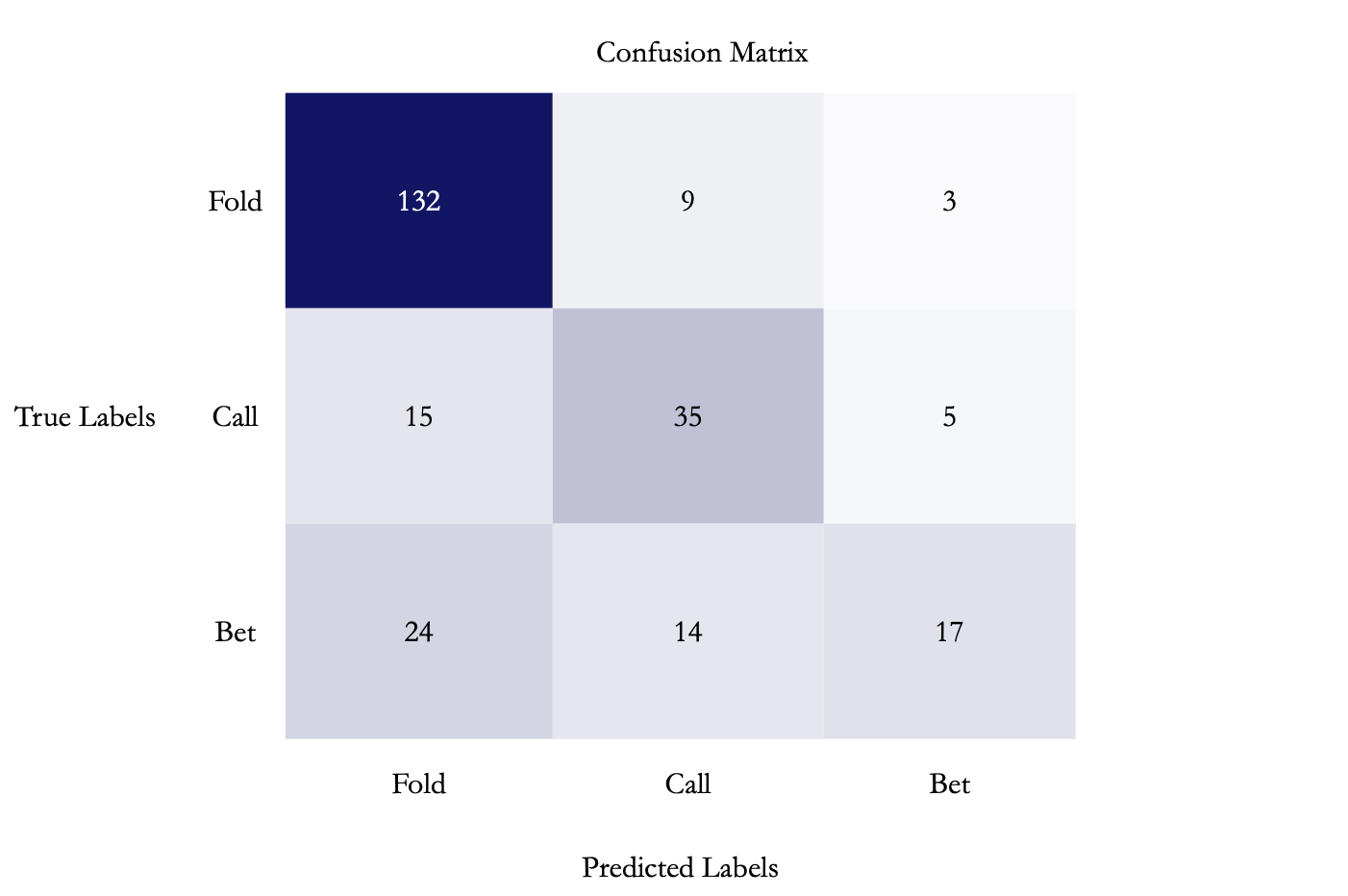
The confusion matrix shows the performance accuracy of the bot:

The bot produced an accuracy of 68.11% when trained with 2571 samples. To further improve the bot’s performance, we made some changes and adjustments to ensure more efficient outcomes and more precise decision-making. First, memory management was optimized using a generator pattern, preventing crashes and enabling the processing of unlimited games instead of being capped at around ten thousand. Hand rankings were converted into probability values, boosting model accuracy by 5–10% thanks to the use of continuous 0–100% values rather than discrete integer categories. Finally, comprehensive error handling and logging were added, allowing the program to skip problematic files and continue running instead of crashing altogether. 

To conclude, we introduced the main game theory concepts behind poker and showed how our bot applies them through neural network–based decision-making. Our model does not use CFR because a full CFR implementation requires very large memory and storage capacity, which was beyond the scope of this project. Therefore, our approach prioritized practicality and efficiency. Instead of attempting to compute equilibrium strategies directly, we focused on building a model that learns from real game outcomes and approximates strong play through pattern recognition, statistical inference, and neural network training. Looking ahead, a compelling avenue for future work would be to explore whether CFR or a tailored, optimized version of it could be incorporated into the architecture. Advancements in abstraction techniques, more efficient sampling algorithms, and better data compression could make it possible to build a CFR-driven bot with significantly reduced computational demands.

References

[1] Neller, T., & Lanctot, M. An Introduction to Counterfactual Regret Minimization. Model AI

Assignments 2013.

[2] Steven Gong’s Notes – “Counterfactual Regret Minimization” and “Game Abstraction” (2025).

[3] Cottingham, J. (n.d.). My attempt at writing a poker bot. Medium.