Portfolio Optimization with Graph Theory

Download PDF

Introduction to Graph Theory

Graph theory is a field of mathematics that explores the properties of graphs, which are abstract representations of a set of objects where some pairs of the objects are connected. In an undirected graph , the set represents vertices (or nodes), and represents edges, which are unordered pairs of vertices. This means that the connection between any two vertices is bidirectional and lacks orientation, making undirected graphs particularly suitable for modeling mutual relationships.

Edges can carry weights , quantifying the strength or significance of the connection between vertices and . The flexibility in defining these weights allows graphs to model a wide range of relationships, making them powerful tools for analyzing complex systems.

Graph Theory in Financial Markets and Portfolio Optimization

In financial markets, graph theory provides a framework for understanding and managing the relationships between assets. By representing assets as vertices and defining edges based on various similarity or dependency measures, investors can visualize and analyze the network of relationships that contribute to systemic risk.

Defining Edges in Financial Graphs

Edges in financial graphs can be defined using a variety of metrics, capturing different aspects of asset relationships:

• Distance Correlation: Unlike Pearson correlation, distance correlation measures both linear and nonlinear associations between assets 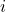and . It takes values between 0 and 1, where 0 indicates no dependence and 1 indicates perfect dependence. It also does not require equal dimesions of time series which is important if we want to be comparing assets with differently sized time series
• Dissimilarity Measures: A dissimilarity metric can be derived from distance correlation:

This metric quantifies how dissimilar two assets are, serving as the weight of the edge between them.

• Assortativity Coefficients: These coefficients measure the tendency of assets to connect with similar or dissimilar assets based on certain attributes, such as industry sector or market capitalization.
• Fundamental Economic Relationships: Edges can represent relationships based on fundamental data like earnings, dividends, or leverage ratios, capturing deeper economic connections beyond market prices.

This flexibility means that edges can be tailored to reflect any relevant relationship, providing a more comprehensive view of how assets interact and contribute to systemic risk.

Advantages Over Modern Portfolio Theory (MPT)

Modern Portfolio Theory, developed by Harry Markowitz, is based on optimizing the trade-off between expected return and risk, using the mean and variance of asset returns. However, MPT relies on several key assumptions:

1. Normal Distribution of Returns: MPT assumes that asset returns are normally distributed, which simplifies risk assessment using variance.
2. Stable Correlations: It presumes that the correlations between asset returns are constant over time.
3. Mean-Variance Sufficiency: The mean and variance are considered sufficient to describe the return distribution.

These assumptions can lead to significant issues:

• Non-Normality of Returns: Financial returns often exhibit skewness and kurtosis (fat tails), deviating from the normal distribution. This can result in underestimating the probability of extreme losses.
• Time-Varying Correlations: Correlations can increase during market stress, leading to simultaneous asset declines and undermining diversification benefits.
• Estimation Errors: Relying on historical means and variances can introduce errors, especially in estimating expected returns, which are notoriously difficult to predict accurately.

Graph Theory Addresses These Limitations.

Graph-based portfolio optimization does not require assumptions about return distributions or expected returns:

• Distribution-Free Framework: By focusing on asset relationships through measures like distance correlation, graph theory sidesteps the need to assume normality of returns.
• Dynamic Relationships: Graphs can be updated frequently to capture changing relationships, providing a more adaptive approach to risk management.
• Multifaceted Edge Definitions: Edges can represent various factors contributing to systemic risk, including non-linear dependencies and fundamental economic ties, offering a more nuanced view than simple linear correlations.

Centrality Measures in Financial Graphs

Centrality measures identify the most influential or critical nodes within a network. In financial graphs, these measures help pinpoint assets that may significantly impact the portfolio’s risk profile.

• Degree Centrality: Counts the number of direct connections an asset has. Assets with high degree centrality are directly connected to many others, potentially amplifying market movements.
• Betweenness Centrality: Reflects the extent to which an asset lies on the shortest paths between other assets. High betweenness centrality indicates an asset’s role as a bridge in the network, which can be critical in the spread of systemic risk.
• Communicability Betweenness Centrality: Extends traditional betweenness centrality by considering all possible paths between nodes, weighted by their lengths and the connectivity of the paths. This measure captures both direct and indirect influences, providing a deeper understanding of an asset’s role in the network.

Portfolio Construction Using Graph Theory

To construct a risk-minimized portfolio without relying on expected returns, we can utilize graph theory in the following way:

1. Build a Correlation Network:
   • Calculate the distance correlation for each pair of assets.
   • Compute the dissimilarity metric:

• • Construct an undirected graph where each asset is a vertex, and edges are weighted by .

1. Calculate Communicability Betweenness Centrality:
   • Use the adjacency matrix of the graph, where .
   • Compute the communicability matrix , where is the matrix exponential of .
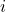   • Calculate the communicability betweenness centrality for each asset , which reflects its overall influence in the network. Intuitevely this measure shows how likely is each stock to spread shocks through the whole system. Nodes with high connectivity can represent a high systematic risk to the network.
2. Assign Portfolio Weights Inversely Proportional to Centrality:
   • Determine the weights 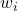as follows:

• • This approach assigns lower weights to assets with higher centrality, reducing exposure to assets that are more central in the network and potentially carry higher systemic risk.

Benefits of This Approach

• Risk Minimization: By focusing on assets with lower centrality, the portfolio is less exposed to systemic risks propagated through highly connected assets.
• No Assumptions on Expected Returns: This method does not require estimating expected returns, avoiding potential errors from incorrect assumptions or estimations.
• Captures Complex Relationships: Using distance correlation and centrality measures that account for all paths in the network allows for a more comprehensive understanding of asset interdependencies.
• Dynamic Adaptability: The graph can be updated with new data to reflect changing market conditions, ensuring the portfolio remains aligned with the current risk landscape.

Using Graph Optimization on DJIA Stocks

In this part, we apply graph optimization techniques to the components of the Dow Jones Industrial Average (DJIA) to construct a risk-minimized portfolio. By leveraging the relationships between stocks captured through graph theory, we aim to improve upon traditional portfolio optimization methods.

Data Collection and Preprocessing

We collected historical daily closing prices for DJIA stocks from 2006 to 2024 using Python’s yfinance library. The dataset spans over 18 years, providing a comprehensive view of different market conditions.

Data Cleaning and Stationarity

To prepare the data for analysis, we performed the following steps:

1. Data Cleaning: Removed any stocks with incomplete data or those that were added to the DJIA after 2006 to ensure consistency.
2. Differencing Prices: Calculated the first difference of daily closing prices:

where is the closing price at time .

1. Ensuring Stationarity: Differencing transforms non-stationary price series into stationary series of price changes. Stationarity is crucial because many statistical methods assume that the underlying data-generating process has constant statistical properties (mean, variance) over time. Non-stationary data can lead to spurious results and unreliable inferences.
   • Augmented Dickey-Fuller Test: We confirmed stationarity using the Augmented Dickey-Fuller (ADF) test, where a p-value less than 0.05 indicates stationarity.

Data Splitting

We divided the dataset into three subsets:

• Training Set (2006–2018): Used to build the initial models and calculate the distance correlation matrix.
• Validation Set (2018–2022): Used to evaluate and compare different portfolio construction methods.
• Test Set (2022–2024): Used for final testing to avoid look-ahead bias.

Splitting the data ensures that our models are evaluated on unseen data, enhancing the robustness of our findings.

Calculating the Distance Correlation Matrix

Using the daily absolute changes in prices from the training set, we computed the distance correlation matrix , where each element measures the distance correlation between stocks and .

Distance Correlation

Distance correlation captures both linear and nonlinear dependencies between variables. Unlike Pearson correlation, it can detect associations even when the relationship is not linear.

The distance correlation between two variables and is defined as:

where:

• : Distance covariance between and .
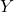• : Distance variance of .

Building the Graph with Threshold

We constructed an undirected graph where each node represents a stock, and edges represent significant relationships based on distance correlation.

Applying a Threshold

An arbitrary threshold of 0.325 was applied:

• Edge Inclusion Criterion:

• Purpose of the Threshold:
  • Noise Reduction: Eliminates weak correlations that may be due to random chance.
  • Focus on Significant Relationships: Highlights stronger dependencies that are more meaningful for portfolio construction.
• Threshold Selection:
  • A lower threshold includes more edges, potentially adding noise.
  • A higher threshold resulted in disconnected nodes, which is undesirable because:
    • Disconnected Nodes: Stocks without any connections cannot be analyzed within the network context.
    • Network Cohesion: A connected graph ensures that centrality measures can be computed meaningfully across the entire network.

Graph Construction

Edges were weighted using the dissimilarity metric:

This metric reflects how dissimilar two stocks are—the lower the value, the more similar the stocks. Bigger nodes indicate a low of connections to other nodes. Edge length shows how dissimilar are nodes.

Calculating Communicability Betweenness Centrality

Communicability Betweenness Centrality (CBC) measures the influence of a node by considering all possible paths through the network, not just the shortest ones. Intuitevely it will help us identify nodes through which risk is more likely to spread. In the plot we can see that stocks such as Walmart or Amazon are relatively disconnected indicating that they will not affect the whole market. General Electric on the other hand is connected to a lot of sectors and can be considered a risky asset.

Allocating Weights Based on CBC

• Inverse Proportionality:

Assigned portfolio weights inversely proportional to CBC:

• Rationale:
  • Stocks with higher CBC are more central and potentially contribute more to systemic risk.
  • By inversely weighting, we reduce exposure to highly central stocks, aiming to minimize risk.

This method follows the approach introduced in Maya Benowitz’s research referenced in the end on the article.

Improving the Method with Minimum Spanning Tree (MST)

To enhance the portfolio, we replaced the arbitrary threshold graph with a Minimum Spanning Tree.

What is a Minimum Spanning Tree?

An MST is a subgraph that connects all the nodes with the minimum possible total edge weight, without any cycles.

• Properties:
  • Connected: Ensures all nodes (stocks) are included.
  • Acyclic: Contains no loops, simplifying the network structure.
  • Minimal Total Weight: Optimizes the overall dissimilarity.

Building the MST

• Edge Weights:

Used the reciprocal of dissimilarity:

• Objective:

Minimize the sum of edge weights:

• Algorithm:

Applied Kruskal’s algorithm to find the MST.

Advantages of Using MST

• Connected Graph: All stocks are included in a single connected network.
• Reduced Complexity: Simplifies the network to the most significant relationships.
• Focus on Highest Dissimilarity: Prioritizes stronger, more reliable connections.

Assigning Weights Based on MST

With the MST, we recalculated CBC but did not invert the weights this time.

• Weight Allocation:

• Rationale:
  • In the MST, central nodes represent stocks that are crucial for maintaining the network’s connectivity.
  • By assigning weights proportional to CBC, we capitalize on the most influential stocks in the simplified network. We can clearly see that nodes Apple, Verizon, United Health and Amazon are the most important for mantaining network connectivity. So we would want to have more of them in our portfolio

Comparing Methods on the Validation Set

We compared four portfolio construction methods on the validation set (2018–2022):

1. Threshold Method: Using the arbitrary threshold graph with inverted CBC weights.
2. MST Method: Using the MST with edges as reciprocal of dissimilarity but proportional CBC weights.
3. Efficient Frontier Portfolio: Constructed using traditional mean-variance optimization.
4. DJIA Index: As a benchmark. But rather than price weighted we use a market cap weigthing mechanism – similar to that of S&P500.

Performance Metrics

The both graph models show similar returns significantly outperforming the Efficient Frontier Portfolio but only slightly the DIJA. Bear in mind that the goal of our portfolio optimization is most importantly managing the risk. Which is why we also evaluated the portfolios using the following statistics:

• Standard Deviation: Measures portfolio volatility.
• Sharpe Ratio: Assesses risk-adjusted returns.

where:

• • : Portfolio return.
  • : Risk-free rate.
  • : Portfolio standard deviation.
• Maximum Drawdown: The largest peak-to-trough decline in the portfolio value.

MST Method Outperforms

The MST-based portfolio has a 24% annualized return over the 4 year period and achieved:

• Highest Sharpe: Outperformed other methods in risk-adjusted return over the validation period (1.08 for MST vs 0.76 for the other graph method vs 0.56 for the EF method vs 0.96 for the Market Cap Scaled DJIA).
• Lowest Standard Deviation: Exhibited lower volatility, indicating more stable performance (20% vs 29% vs 22% vs 22%).
• Lowest Maximum Drawdown: Demonstrated resilience during market downturns (25% vs 27.5% vs 34.6% vs 29.15% during COVID).

Importance of Maximum Drawdown

• Risk Management: Max drawdown reflects the potential loss an investor could experience, crucial for risk-averse investors.
• Psychological Impact: Large drawdowns can lead to panic selling; minimizing drawdown helps maintain investment discipline.
• Recovery Time: Portfolios with smaller drawdowns recover losses faster, improving long-term performance.

Interpretation

• Effective Risk Minimization: The MST method’s focus on minimizing dissimilarity and leveraging centrality measures contributed to superior risk-adjusted returns.
• Robustness: The method proved effective even when market conditions changed, as evidenced by its performance on unseen data and big markets shocks such as COVID.

Testing on the Test Set

To ensure the robustness of the MST method, we evaluated its performance on the test set (2022–2024), which was not used in model selection to avoid look-ahead bias.

• Avoiding Look-Ahead Bias: By selecting the best model based on validation performance and then testing it on new data, we obtain an unbiased assessment.

Performance on the Test Set

• The MST portfolio continued to outperform the DJIA index.
• Maintained lower volatility and drawdown, confirming the method’s effectiveness.

The model outperforms the DJIA even in the period when the market is not showing a clear trend.

Final Analysis and Visualization

Combining the validation and test sets, we plotted the cumulative returns of the MST portfolio and the DJIA index.

• Visualization: The plot illustrates the superior growth trajectory of the MST portfolio over the combined period.
• Consistent Outperformance: The MST method consistently delivered better returns with lower risk.

Next steps

Potential future articles on this topic could include (1) extension of the tradeble universe to introduce uncorrelated assets, (2) comparison of centrality measures and most importantly (3) looking at relationships beyond correlation.

References

1. Federica Ricca & Andrea Scozzari, “Portfolio optimization through a network approach: Network assortative mixing and portfolio diversification”, 2024
2. Benowitz, Maya, “Hedgecraft Part 1: Building a Minimally Correlated Portfolio with Data Science”, 2019