Currency Markets and Filtered Beer (BEER Model)

Download PDF

Introduction (to Exchange Rate Models)

Exchange Rate Models are widely used by entities ranging from central banks to international financial institutions to assess exchange rate misalignments. Strong and persistent departures from equilibrium levels are thought to have a substantial bearing on growth prospects, price dynamics, or even financial stability, but also present attractive relative trade opportunities which we try to exploit in this article.

In a previous article named “Optimization methods for entry and exit points in relative value trading”, we already touched upon the implementation and performance of mean reversion strategies, based on a purchasing power parity framework (PPP). PPP is arguably the most popular approach to monetary theory, based on the assumption that currency returns should be driven by cross-country inflation differentials. However, in this article we explore the predictive power of an alternative approach to assess exchange rate misalignments, using the BEER model and again testing whether these deviations exhibit a mean-reverting behaviour and whether such dynamics can be exploited.

Behavorial Equilibrium Exchange Rate (BEER)

The BEER model, also known as Behavioural Equilibrium Exchange Rate Model, is one of the three main exchange rate frameworks that uses a set of economic fundamentals to calculate the equilibrium exchange rate through a single-equation, time-series approach. In other words, it is a modeling strategy designed to explain the actual behaviour of exchange rates in terms of relevant economic variables.

In contrast to the PPP approach–which is often considered an unreliable measure due to the combination of high real exchange rate volatility and the slow mean reversion of real exchange rates, commonly referred to as the “PPP puzzle” — the BEER model accounts for the sources of this slow mean reversion and the persistent deviations from PPP. The explanatory variables in this model, drawn from economic fundamentals, are selected on the basis of relevant economic theory or empirical studies. However, once the econometric analysis begins, the direct theoretical or empirical link to these fundamentals is no longer preserved. Instead, the equilibrium exchange rate in the BEER model is determined by econometric analysis rather than by theory alone.

Our Data

The dataset of our BEER model consists of data from 2010-01-01 to today. covering weekly returns from the DXY (Dollar Index), both daily and weekly returns from the VIX and MOVE Index, the respective FX rate and its quarterly momentum. Furthermore, we also used yearly CPI, GDP and Unemployment Percentage differences between the respective countries, as well as the respective Equity Index of the currency area (e.g. the S&P for the US or the FTSE for the UK). Additionally, we used the differentials of yield levels for the benchmark government bonds, for the maturities 3M, 2Y, 5Y, 10Y, and accounted for the steepness in yield curves between the respective countries.

Now diving a bit into the economic intuition behind our choice of explaining variables, our first variable, the weekly returns of the DXY, was chosen due to the simple fact that its returns reflect broad shifts in the global demand for USD, driven by various underlying reasons such as trade flows, capital allocations, interest rate differentials and investor risk sentiment.

Furthermore, when building an equilibrium exchange rate model such as the BEER model, the bilateral rates of the USD with different currencies are not just influenced by the fundamentals of the currency areas but also by the general strength or weakness of the USD. The VIX index, which measures the forward-looking implied volatility of S&P 500 options, and the MOVE index, which displays the implied volatility of US Treasury yields, both have a significant impact on USD equilibrium exchange rates. In risk-off periods, investors historically rushed into safe-haven assets, with US Treasuries being the most popular. On the other hand, a higher risk appetite supports investors entering opportunities in higher-yielding currencies and therefore supports currencies other than the USD. In addition, we used both daily and weekly returns, as daily returns capture short-term shocks, helping our BEER model account for USD demand shocks linked to investor sentiment. Weekly returns capture more persistent sentiment shifts and smooth out random intraday volatility, which is often irrelevant for the equilibrium exchange rate.

We also used fundamental macro data in our model, including YoY differences in CPI, GDP and unemployment data between the US and the respective currency areas we are analyzing. For example, if US inflation rises faster than inflation in another country, the USD tends to depreciate in real terms over time, because US goods become relatively more expensive, and vice versa. Inflation differentials capture relative price competitiveness and are closely related to PPP fundamentals briefly touched upon earlier. Stronger GDP growth, on the other hand, indicates stronger fundamentals, leading to capital inflows, implying better fiscal sustainability, and is also often linked to the Balassa-Samuelson effect. Lastly, a relatively lower unemployment rate signals a stronger labor market, which supports domestic demand and monetary policy tightening, leading to stronger exchange rates.

In addition, we considered the daily changes of the major index level of each country, as they capture broad market sentiment and macro fundamentals. For example, a rising S&P 500 level relative to other markets typically attracts foreign investment, which leads to stronger capital inflows and therefore USD appreciation.

A similar reasoning applies to why we used both the differences in yield levels between different government bond tenors of the included currency areas and the differences in the steepness of the respective yield curves. A higher short end of the yield curve, especially in the US, leads to capital flows towards the US as the expected returns on Treasuries increase, supporting USD appreciation. Long ends, on the other hand, reflect growth and inflation expectations as well as sovereign risk and other factors, also impacting exchange rates. Furthermore, the difference in yield curve steepness gives us further insight into policy path expectations and term premia, both influencing exchange rate levels.

Lastly, we also incorporated the momentum over 21 days (monthly) of the respective currency pairs, as exchange rates often exhibit short- to medium-horizon trend persistence due to slow information diffusion, hedging programs, and flow autocorrelation as corporates, asset allocators, and reserve managers rebalance infrequently (monthly/quarterly), generating persistent flows that move FX beyond what contemporaneous macro variables explain. We used a monthly horizon, as shorter windows are often too noisy, raising false signals and overfitting, while longer windows lag in identifying turning points. In addition, this time horizon complements the daily, weekly, and monthly fundamentals, thereby bridging our analysis.

The Strategy

We design the strategy as a time-varying BEER with USD denominated FX pairs: We use a Kalman filter that yields an out-of-sample forecast–the residual between actual and fitted return–which we standardize with a 52-week z-score and trade mean reversion around: we short when the z-score is sufficiently positive, buy when it is sufficiently negative (0.5 standard deviations in our case), and exit toward zero. To avoid fading persistent moves, we scale the position with a 1-month momentum dampener: empirically, across our pairs crosses the strongest trend persistence sits in the ~3-weeks to ~3-months window, and a 1-month lookback also captured those medium-horizon trends dominate without over-penalizing short, noisy bursts.

We also impose a carry-control rule (we don’t put on positions that pay adverse funding) because in currencies, carry can overwhelm a slow mean-reversion edge. We report PnL on a simple $100k notional per trade. Costs are deducted using IBKR’s $2.95 per side to reflect realistic commissions; signals are formed on weekly data and implemented either at the next weekly bar or carried over daily bars, with costs charged only when the position changes.

For simplicity and due to our time constraints, we chose simple, fixed entry/exit bands for the article, which is mildly forward-looking and therefore optimistic; costs are flat, and weekly risk is held through the week. If we were hardening this, we’d fit bands out-of-sample with a rolling optimization, either mapping z-scores to positions via a rolling sigmoid (learned slope/center) or modeling the residual as an Ornstein-Uhlenbeck process and deriving profit-optimal boundaries from its estimation.

We’d also let different feature blocks adapt at different speeds by estimating process vs. measurement noise in the Kalman layer. Even with these simplifications, the sleeve captures a small, persistent edge with near-zero equity beta–exactly the sort of orthogonal return stream that adds value when diversified across pairs.

Why We Use Kalman Filters (and not just rolling OLS)

FX relationships aren’t static. Risk premia, carry, and macro sensitivities drift across macro and rate cycles, policy regimes, and volatility regimes. A Kalman filter lets us model that drift explicitly. For the sake of intuition, one can think of a Kalman filter as a more cutting-edge ridge regression with multiple advantages when it comes to non-stationary time series data.

On an interesting side note, Kalman has been used as a tool for some of the early Apollo missions in the 60’s and continues to be used outside the realm of quantitative finance for things like autonomous navigation, including for nuclear submarines and Tomahawk missiles.

Now, we write our time series of FX returns as a time-varying linear model:

, with coefficients that evolve as

.

where, is the market noise, and (process noise) controls how quickly betas are allowed to move, with a higher

This gives us:

• Adaptive betas. Unlike static/rolling OLS, the filter updates 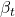every step. It “learns” during regime changes and stabilizes in quieter markets (we tune the speed/adaptiveness with the process-noise/“forgetting” parameter).
• OOS (out-of-sample) estimation. The recursion produces a one-step-ahead forecast and an innovation we use as our trading residual.
• Noise handling and shrinkage. The covariance functions as a probabilistic ridge penalty when the features show multicollinearity, further reducing overfitting.
• Flexible extensions. Different blocks (carry, momentum, rates vol) can have separate dynamics by adjusting their process noise. However, we have decided not to implement this in our model due to time constraints.

In practice, this often yields smoother and more robust residuals OOS for mean reversion than rolling regressions–especially around larger macro regime shifts where static BEER models can falter.

Results

Our Kalman-BEER fade with momentum dampener delivers a steady PnL profile for the pairs tested. The average R-squared across pairs was around 0.05-0.10, meaning we explained a good amount of the variance in returns.

To be concise, we’ll go a slightly more in depth on the USD/GBP pair and show the numbers for the others: the strategy posts an annualized return ~3% with vol ~6% for a Sharpe ≈ 0.46, a max drawdown ~14%, and a beta to the S&P 500 of about -0.02 (i.e., essentially zero). Annualized alpha versus the S&P is ~3%, consistent with the strategy earning returns that are orthogonal to equity risk.

Skewness ≈ +0.68 (right skewed): returns have a mild tendency to deliver larger positive than negative outliers. That’s intuitive given our overlays: we avoid shorting positive-carry currencies and scale down when trend is strong, which truncates some left tails while letting mean-reversion wins run.

Kurtosis ≈ 10.3: returns are leptokurtic (fat tails). FX can sit in narrow ranges for weeks and then gap on macro news (policy surprises, UK-specific events). This validates our risk design–vol targeting and entry/exit thresholds–because simple variance assumptions would understate tail risk.

Since the Kalman layer lets betas drift, we adapt fairly well across policy cycles (Brexit era, 2020-22 vol, the recent BOE tightening). That’s visible in the rolling Sharpe and the resilience outside the few sharp drawdown windows.

The strategy’s beta ~0 and typically low correlation to other macro factors make it a good portfolio diversifier. Diversified across many pairs, the book-level Sharpe can rise materially as idiosyncratic shocks diversify out. We show graphs for JPY and SEK as examples of pair results and show visually that a similar explanation of results can be made. A table of results across pairs can also be found below.

JPY (Japanese Yen)

SEK (Swedish Krona)

All Pairs

All in all, across GBP, SEK, JPY, and CHF the strategy delivers mid-0.3 to mid-0.4 Sharpe with near-zero beta (-0.04 to +0.04), showing genuinely diversifying returns. Max drawdowns cluster in a -12% to -16% range–manageable given some vol targeting. Skew is positive for most pairs (GBP 0.68, CHF 0.35, JPY 1.37), consistent with the momentum dampener and carry filter trimming left tails; EUR is the exception with negative skew. Kurtosis is elevated everywhere (7-26), reminding us FX returns often come in short bursts; JPY’s very high kurtosis (26) fits a regime with BoJ yield-curve control and intervention.

An outlier here is that EUR/USD seems structurally harder for this setup. The euro is a monetary union of heterogeneous economies, so area-wide aggregates (growth, inflation, unemployment, curves) blur country-level info. Hence, our US vs. foreign differentials are noisy and less mean reverting. Long policy-driven swings (ECB QE/negative rates, the 2022 energy terms of trade shock) and our carry-control filter here seems to often block the USD-long trades that dominated big trends. The result is a low Sharpe (~0.10) with left skew (-1.11) and very fat tails (kurtosis ~18).

Overall, however, the strategy shows a small, persistent edge across several pairs with low market correlation.

Conclusion

To conclude, we have shown equilibrium-based strategies can be made more robust by combining economic fundamentals with adaptive filters and trading overlays, bridging the gap between purely theoretical BEER models and implementable trading strategies. In general, the strategies’ near-zero beta to equity markets, stable OOS behaviour, and typically low correlation to other macro factors make the strategy a promising portfolio diversifier for a multi-asset or multi-cross macro book.

However, we also acknowledge that there are multiple areas we could improve upon. Firstly, we could have improved upon our feature engineering by batching certain features, such as rates and macro data, better or perhaps transforming them using Principal Component Analysis to further avoid multicollinearity. Adding onto that, it also makes sense to explore non-linear transformations of variables, since FX drivers may interact in non-additive ways. Furthermore, implementing the strategy on more currency pairs would materially diversify out idiosyncratic risk and hence also increase the book-level Sharpe Ratio. We could also further optimize our entry and exit thresholds, using regime-dependent boundaries, estimated for example from an Ornstein-Uhlenbeck process, instead of using fixed z-scores.

For future analysis, it would be interesting to test the framework on EM currencies, where structural misalignment and carry premia are often even larger, further exploring portfolio optimization across pairs to maximize diversification benefits.

References

[1] Ca’ Zorzi, M., Cap, A., Mijakovic, A., Rubaszek, M., “The predictive power of equilibrium exchange rate models”, European Central Bank Working Paper Series, 2020