According to the Financial Times, Credit Derivatives market was a $10 trillion market in the beginning of 2017. While this figure has taken a bump from a heyday before the Great Financial Crisis a decade ago, it makes for an essential cornerstone of the finance world. This article will proceed in the following manner. We will first explain the basics of a CDS. Then we will move on to highlight some unconventional uses for the CDS and finally, explore an interesting concept that can affect portfolio balancing during times of economic crisis. Arguments presented in the last section are done keeping in mind the various regulations that the Basel III contains. The results obtained will affect the portfolio re-balancing to keep within regulatory requirements of the Value-At-Risk for institutional investors.
CDS basics
Credit Default Swaps belong to the category of derivatives, financial instruments whose value depends on another entity. More specifically, CDS contracts are credit derivatives, which are used by buyers to get protection against credit risk. CDS contracts are mainly purchased by banks willing to obtain insurance against the possibility of deterioration of the credit quality of the entities to which they lend. Conversely, CDS contracts are mainly sold by those institutions willing to get some exposure to credit risk only, without having to raise funds.
The buyer of a CDS pays a lump sum or a periodical amount of money to the seller, who in turn will make a payment if a certain credit event occurs. Bankruptcy or other objectively measurable occurrences are the main credit events that trigger the payment by the seller of the CDS. If another event occurs, which is not explicitly foreseen in the contract, the seller does not have any obligation to make payments. This disbursement may take two forms: cash settlement and physical delivery. In the former case, the payment is equal to the difference between the par value of the underlying asset (a bond, a loan or some other debt) and its value after the credit event; in the latter case, the payment is equal to the par value of the asset, but the holder of the CDS must deliver the underlying. In other circumstances, however, the settlement may take the form of a cash payment, which has been predetermined, either by formula or by a fixed amount.
One of the first benefits of CDS contracts is the possibility of better diversifying risk. If bank A mostly lends to oil-producing companies, it might suffer multiple losses if the oil-producing industry performs poorly. By using CDS contracts, bank A will be able to buy protection from some of its loans and sell an equal value of CDS contracts which are tied to loans to, let us say, agricultural firms. The result of this strategy is a lower risk on the overall loan portfolio. This strategy is commonly referred to as “income-neutral credit diversification”. The best scenario occurs when the correlation coefficient between the two default rates is low and when the underlying loans share similar characteristics (interest rates, credit quality, etc.). Swaps can also be used to exchange default protection between two lenders. This is another very efficient method to diversify risk. If two banks have a loan portfolio which is very exposed to a single risk factor, they can mutually purchase CDS contracts on a portion of their loans and get exposure to the risks of the other bank.
Usage of CDSs under capital regulations to increase firm’s ROE
CDS contracts can also be used to manage regulatory capital and to improve return on capital. According to international regulations, banks must keep a minimum amount of capital, which is computed as a percentage, usually 8%, of its risk-weighted assets. Each asset has its own weight, therefore if bank A holds riskier assets (such as credit card loans) it will have to raise capital. On the other side, if bank A only holds government securities, which are less profitable but safer, it will have looser capital requirements.
Let us take the example of two banks: bank A and bank B. Bank A, which is considered safer by the market, can fund its loans at LIBOR minus 25 basis points, while bank B, which is less safe, can fund its loans at LIBOR plus 25 basis points. The two banks can lend $50 million to a corporation at LIBOR plus 50 basis points. The risk of the loan is the same for both banks, so they will have the same capital requirements on this asset, whose weight is 100%. Therefore, the capital requirement is $4 million (8% of $50 million). If LIBOR is equal to 5.50%, both banks will receive an interest rate of 6% (5.50% plus 0.50%), which corresponds to $3 million each year. Both banks can raise just $4 million of capital and borrow the remaining $46 million. Bank A will pay $2.415 million (5.25% of $46 million) of interests each year, while bank B will pay $2.645 million (5.75% of $46 million). The net interest income for the two banks will be respectively $0.585 million ($3 million minus $2.415 million) and $0.355 million ($3 million minus $2.645 million), implying a return on capital of 14.625% and 8.875%.
Given this scenario, let us see how it can be improved by using CDS contracts. Bank A, which has the lowest funding costs, will lend $50 million to the firm. Bank A, subsequently, will buy a CDS on that loan from company B, which will receive 50 basis points (the measure of credit risk) each year from bank A. If the company will default, bank B will make a cash settlement. The only credit risk that bank A faces is related to the possibility that bank B will not be able to make the cash settlement in case of credit event. Bank A faces a much lower risk now, as the probability that B will default if also the borrowing firm defaults is low.
According to international regulation, the minimum capital bank A must keep is lower now (the risk weighted asset is now $10 million, 20% of $50 million). The new minimum capital is $0.8 million (8% of $10 million). Bank A will be able to borrow $49.2 million, paying $2.583 million (5.25% of $49.2 million) plus the CDS premium of $0.25 million (0.5% of $50 million). Interest income will be the same as in the previous scenario, so the net interest income will be $0.167 million ($3 million minus $2.583 million minus $0.25 million). Return on capital is equal to 20.875%, much higher than before.
On the other side, bank B receives $0.250 million of income. According to regulators, its capital must cover 8% of the $50 million the bank must pay in case of default of the company. The minimum capital requirement is therefore $4 million, which can be invested in cash equivalents like Treasury notes yielding 5.25%, which is $0.210 million a year (5.25% of $4 million). The resulting return on capital is 11.50%.
For both banks, the use of CDSs means higher returns on capital.
Commonality between Credit Default Swap Spread (GFC) [1]
This section picks up on the increase in the co-movement between credit default swap (CDS) spread changes during the 2007–2009 crisis and investigates the source of that increase. While we will present the technique to isolate various factors in order to come to the results, readers can refer to Anderson (2017) for all other calculations and tabular results. The data set includes the daily spreads for 159 liquid investment- grade corporate single-name CDS contracts from Dec. 23, 2005, to Mar. 9, 2009. These contracts are included in the CDS North American Investment Grade Index (CDX.NA.IG) rolls 8–12. The tests show that fundamentals accounted for only 23% of the increase in covariance. The remaining increase is attributed to changes in liquidity and the market price of default risk. On the other hand, counter-party risk played an insignificant role in the spreads.
Dissertation of the factors that affect the spreads during times of crisis must be studied for a number of important reasons. First, an increase in the co-movement in spreads takes away the ability of investors to diversify risk in times when it is most required. Intuitively, this is because diversification of risk in financial markets is limited by the level of commonality between asset price movements. Second, increased commonality can force the institutions to deleverage their balance sheet to shed risk. Raising capital or shedding risk during times of increased commonality would incur transaction costs. As shown through the article, financial institutions need to understand the factors that drive this commonality for if it is the result of short-term factors, keeping portfolio allocations unchanged might be cost-effective and in the long-term interest of the managers.
To get more robust results, the contracts are divided into quintile portfolios based on Moody’s KMV expected default frequency (EDF) measure. Covariances are then decomposed into fundamental and excess components to get a better idea of movements. This is carried out using a linear factor model with covariates implied by Merton (1974). The author finds that the covariance between portfolio CDS spread changes increased 70-fold over its pre-crisis level on average, resulting in a $2.5M increase in value- at-risk (VaR) for a portfolio of 60 CDS contracts. However, only 23% of the increase in covariance relates to fundamentals. The remainder can largely be attributed to changes in liquidity and the default risk premium, which account for an additional 10% and 18% of the increase, respectively. When time-varying factors are accounted for, the model captures 66% of the increase in covariance compared to 45% with constant parameters. Even after that, the 34% of increase in co-variance that is left unexplained is attributed to Lehman’s failure and disappears with the time-varying inclusion within 6 months of the event.
Model Method
The results are obtained by dividing the data into quintile portfolios in order to reduce the noise of data. These portfolios are rebalanced on the last day of each month according to the prevailing EDF. The portfolio spread, on each day of the subsequent month, is simply the equal-weighted average spread over contracts in the quintile. The formula used is
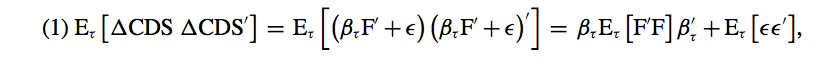 Source: Allen and Saunder (2003)
Source: Allen and Saunder (2003)
where CDS is an M × 1 vector of portfolio CDS spread changes, βτ is an M × K matrix of factor exposures, F is a 1 × K vector of factors, and ε is a M × 1 vector of residuals. The subscript τ = {precrisis, crisis} in the baseline analysis.
In simple terms, all that the equation is telling us is that all else equal, changes in spreads can only be due to a change in three things: 1. an increase in exposure(s) to a common factor, 2. an increase in Eτ[ F′F] , and 3. an increase in covariance between unexplained CDS spread changes.
Systematic proxies for the fundamental factor evaluation of the delta CDS that can give us a better idea about the expected default rate are given by the following formula:
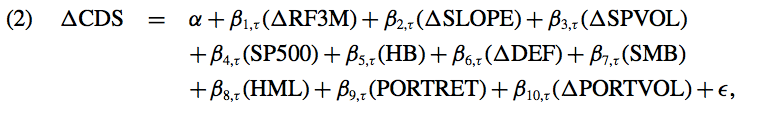
Source: Allen and Saunder (2003)
where RF3M is the 3-month risk-free rate, SLOPE measures the slope of the yield curve, SPVOL is the generalized autoregressive conditional heteroscedasticity (GARCH) volatility of the S&P 500 index return, SP500 is the S&P 500 index return, and HB is the return for an index of U.S. home builders. DEF is the yield difference between Moody’s Baa and Aaa seasoned bond indices. SMB and HML are the small cap and value premiums, respectively. PORTRET is the equal- weighted equity return for the EDF-sorted quintile portfolio. PORTVOL is the GARCH volatility of PORTRET.
Results and Conclusion
Three most important takeaways that emerge are as follows:
- Exposures to SP500, RF3M, and HB increased monotonically across EDF-sorted portfolios. This suggests that increased credit risk specifically linked to changes in macroeconomic conditions. The risk-neutral drift and housing market conditions increased the covariance be- tween all portfolio pairs in the crisis;
- The change in exposure to DEF is insignificant across all portfolios. This is in line with the view that DEF is a coarse measure of credit market conditions rather than a precise proxy for the default risk premium (Gilchrist and Zakrajsek (2012));
- Exposure to HML became insignificant across all portfolios during the crisis. This may represent a decoupling of the CDS and equity market over this time period.
The study also points out that covariance levels were different during different periods of the crisis. While we explored the ‘what’ behind constant covariance changes, the variations in different time intervals can be attributed to changes in fundamentals, liquidity, and the default risk premium with monthly time-varying exposures. However, in the 6 months following the failure of Lehman Brothers, covariance spiked beyond what could be explained by the model.
One important result explodes out of this study. Basel III introduced specific capital charges for “stressed” VaR and correlation trading portfolios, calling for 12 months of historical data in the VaR calculation. The study finds that the estimation window could be an important consideration in adequately capitalizing credit derivative trading books under economic distress. Capital held against stressed VaR for CDS contracts and for correlation trading portfolios will likely combine charges for both credit and non credit-related covariance. Large changes in covariance linked to extreme events are likely short-lived. Therefore, investors may incur unnecessary costs by reallocating to offset large short-term changes in covariance. It is prudent to consider the sources of increased covariance in the reallocation decision.
[1] The last section of this article is an adaptation of comparative strategy method used in research by Mike Anderson in his recent publication in Journal of Financial and Quantitative Analysis. Ideas presented here are re-constructed from the arguments present in the paper



0 Comments