How to Trade Football Clubs: A Case Study on Juventus

In this article we analyze how to set up trading strategies on listed football clubs exploiting the peculiar behaviour of returns and implied volatility in correspondence to UEFA Champions League matches. In particular, this article is structured in four parts. In the first part, we briefly introduce the link between revenues of clubs and the results of UCL games. In the second part, we verify empirically whether the relationship between returns and outcomes of UCL matches is statistically significant through an event study. Then, in the third part we show how UCL games affect implied volatility and we backtest two trading strategies, which try to exploit this phenomenon. Finally, in the fourth part we present how you could set up a sort of arbitrage using sports bets and options, we also report empirical results for this strategy.

1. Introduction
In the past football clubs used to be poor investments. Usually, there were local benefactors injecting cash into loss-making football teams for reputational reasons and to gain visibility in their communities rather than for profit.
In the last decades the media revolution transformed football clubs into entertainment companies with relevant revenues and balance sheets.
Furthermore, at the same time, we have seen several football clubs being listed in the market. Nowadays, there are 22 listed football teams worldwide. For instance, in Italy there is Juventus (since December 2018 it is part of the Ftse Mib), Lazio and Roma while in England there is Manchester United and in Germany Borussia Dortmund.

However, if you look at historical returns of listed clubs they have shown a quite weird behaviour. In fact, apart from not distributing dividends to shareholders, they seem not to be very responsive to the fundamentals of the company, such as the level of debt or profitability. On the contrary, they appear to be very sensitive to the results of football matches, especially the most important ones such as those of the knockout stage of UEFA Champions League. Behind this behaviour, at least for UCL, there could be an economic logic, because for every victory in a UCL match the club gets a money prize. They can have a relevant impact in the income statement of a club, for instance, two years ago, when Juventus reached the final of UCL they got more than €100 million as money prizes, representing about 20% of total revenues.
In the tables below it is indicated how much clubs get for every victory in both the group stage and the knockout stage of UCL:

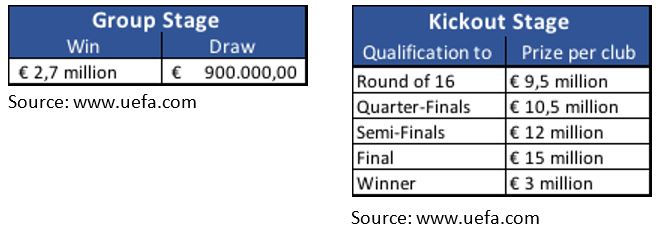
Moreover, UCL matches, especially in the knockout stage, don’t influence revenues only through money prizes but also through the number of tickets sold: the further you go into the competition, the more games you play. Finally, UCL matches allow clubs to have an international exposure and gain visibility and reputation through which they can close better deals with sponsors, attract the best players and sell more merchandise.

Once we have understood the economic logic that could justify the link between games results and returns, we tried to verify empirically whether outcomes of matches have actually a statistically significant impact on returns of listed clubs through an event study.

2. Event study

An event study is a statistical method used to investigate the relationship between security prices and economic events (Dyckman et al., 1984). These kind of studies are usually used to test whether the stochastic behavior of stock prices is affected by the disclosure of firm-specific events such as mergers, acquisitions or earning announcements. Similarly, we use the same approach to test whether Juventus returns are affected by the outcome of matches in Champions League. 


Our event study is basically a statistical hypothesis test with the following null and alternative hypothesis:

H0: The outcome of matches does not affect the return of the stock

H1: The outcome of matches has a significant impact on the return of the stock

Before proceeding with the test, we made some choices regarding the data to use. First of all, we used data of Juventus Football Club, because it is one of the largest European clubs which are listed and in recent years it has often participated at the knockout stage of UEFA Champions League reaching the final twice. The most relevant reason why we chose Juventus is that at the end of 2018 it has been added in the major index of Italian stock market, the Ftse Mib, and therefore it has listed options. Since we wanted to set up some trading strategies with options we needed listed options.
Then, we considered as events only matches of the knockout stage of UEFA Champions League, because their outcome can affect directly and substantially the income of the club.
Finally, we considered only those cases where the club lost and not when it won. We made this choice because the impact of losses on prices tend to be stronger. In fact, when you lose a match you don’t lose only the money prize associated with that turn but also all the money prizes you could have won in future stages.

We used data regarding the last six seasons of UCL (including 2018/2019 season). In this period Juventus played a total of 26 matches in the knockout stage and out of them, 10 were defeats. We considered as defeats also draws with home court and second turn matches where Juventus won the turn but it lost the match anyway. The matches in our sample are indicated in the table below:

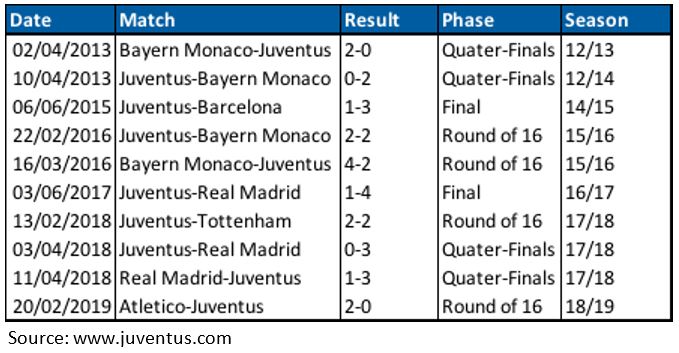
We measure the effect of every match on stock returns through what is called “abnormal return”. Abnormal return is the difference between the actual return of the stock and its expected return over the same period:

Abnormal \: Return_t= R_t - E(R_t)

where R_t is the log return from t-1 to t

As far as the expected return is concerned, you can compute it in many different ways. We decided to compute it using a simple market model, according to which the expected return of a stock is a linear function of the return of the market measured in the same time interval:

E(R_t)= \alpha + \beta R_{M,t}

where \alpha and \beta are the parameters of the model and R_{M,t} is the log return of the market between t-1 and t.
As a proxy of the return of the market we used the log return of Ftse Mib.

We want to verify whether the abnormal returns after the club has lost the match are significantly negative. Hence, the hypothesis test we introduced at the beginning of this section can be written more formally as follows: 


H₀: Abnormal returns = 0
H₁: Abnormal returns < 0

In order to compute abnormal returns, we considered two different time periods, an estimation period and a test period (see the scheme below). The estimation period is represented by 256 trading days ending 20 days before the date of each match (we used 20 days as a buffer so to be sure that our estimation of betas and alphas is not affected by the match). For every game in our sample, we used data in the estimation period to estimate betas and alphas by simply regressing the log return of Juventus against the log return of the Ftse Mib.
The test period is represented by 3 days before and 3 days after each match. Here, for every match in our sample, we used our estimates for beta and alpha to compute expected returns for each day in the test period and, given the actual returns of those days, the corresponding abnormal returns.

For every day in the test period we compute the average abnormal return and the corresponding t-ratios in order to verify whether they are significant at a confidence level of 99%. Results are summarized in the table below:

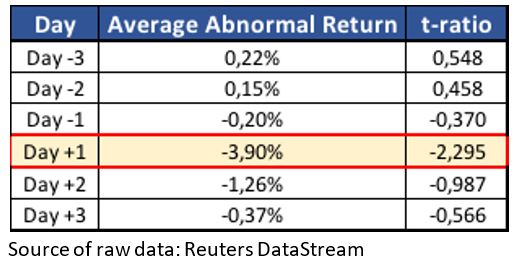
As you can see in the table, on average the day after a defeat in a UCL match of the knockout stage Juventus experienced a negative abnormal return of 3.90%, which is significantly different from zero at a confidence level of 99%. Therefore, we can conclude that results of UFC matches in the knockout stages (at least defeats in the first round) affect significantly returns of the stock. 


3. Trading Strategies  

3.1 Implied Volatility Patterns
The outcome of UCL matches of the knockout stage will materially affect the financial performance of the football team through the money prizes and the increased visibility obtained by the teams winning matches and moving to the following stages of the competition. The day after the match, investors will quickly factor in the stock price the new information represented by the outcome of the match. Given the financial relevance of UCL matches and as we have shown with the event study, we expect large negative or positive returns after the match. Since UCL matches are scheduled events and investors expect big price moves in either directions, for the stocks of the football teams involved, demand for options will rise. Investors use options (especially put options because the standard investor has a long bias) to hedge the risk of large short-term price movements associated with the match outcome. As we approach the match day, higher option demand will push up option prices and lead to a higher implied volatility. Implied volatility will peak on the match day and drop thereafter. The implied volatility drop after the match occurs because new information has been factored in the stock price and uncertainty disappears.

Empirical evidence supports our views. The graph below reports implied volatility movements of Juventus options in the last 2 years. The vertical red lines represent the 6 UCL matches of the knockout stage played by Juventus in the sample considered. We agree on the fact that the sample may look small since it includes only 6 relevant events. However, this is the largest sample available for our analysis since options on Juventus stock start trading only in November 2017. As we notice from the chart, implied volatility behaves as expected, spiking on the match day and dropping the following day. The only exception is the first event: Juventus-Tottenham of 13/02/2018, round of 16. In fact, implied volatility spikes after the match, though the chart can deceive the reader.

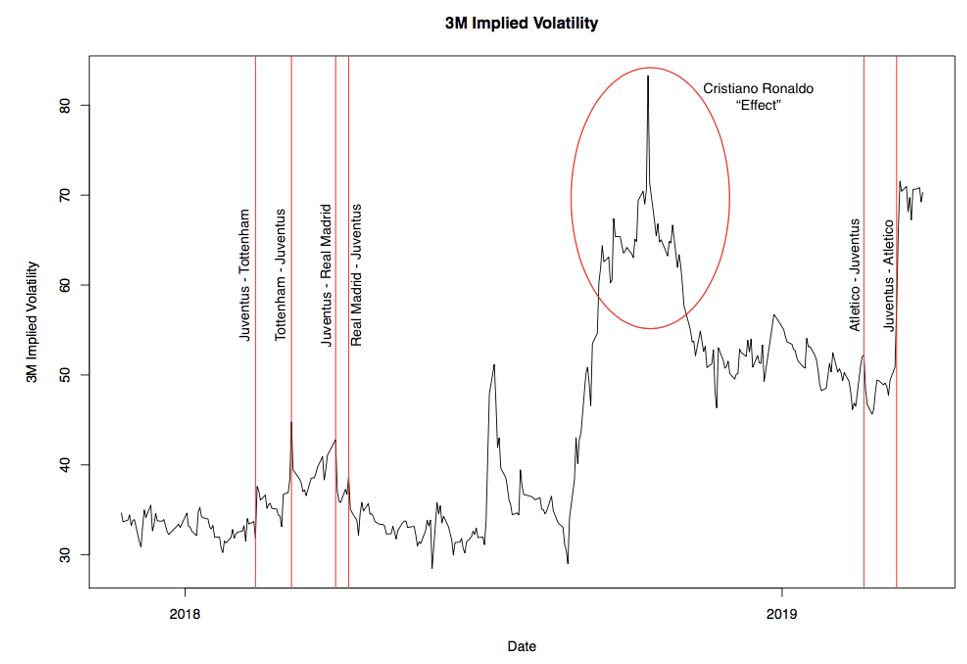
The volatility spike and crush pattern experienced by Juventus stock around UCL match days resembles what we traditionally observe around earnings announcements. On the earnings date, investors will assess the company earnings against consensus, bidding up the stocks if earnings beat consensus and dumping it if earnings miss consensus. The paper by Gao, Chao and Xing, Yuhang and Zhang, Xiaoyan (2017) shows that 20 days before the event implied volatility starts raising, it peaks on the day before the earnings announcement and drops the following day to the normal pre-earnings levels.

3.2 Short or Long Straddle
In order to trade these peaks in implied volatility we need to set up trading strategies based on options. As we pointed out, the pattern in implied volatility in correspondence of match days appears to be quite similar to that you observe during earning announcements. The typical trade you use to profit from earning announcements is a short straddle, where you take a short position on both call and put options, on the same underlying and at the same strike price. Since both call and put options have a positive sensitivity to the implied volatility (positive vega) then, by selling them, you get a negative exposure to it. Therefore, since you are betting on a decrease in implied volatility, you should open the position on the match day when the implied volatility reaches its maximum, due to the uncertainty on the match result and close it the day after when there is no more uncertainty and the implied volatility returns back to normal levels.
Academic research shows that systematically selling straddles generates positive returns. This positive return should not exist in a risk-neutral world. However, since investors are risk averse, option sellers require a risk premium to sell protection, so that we can interpret the positive return generated by systematically selling straddles as a risk premium.

An alternative trading strategy you could use is a long straddle, where you buy both call and put options on the same underlying and with the same strike price. In this case you have a positive exposure on the implied volatility (you have positive vega), betting on an increase of it. Therefore, you should open this position the day before of the match when the implied volatility is still at normal levels and close it in correspondence of the match day when it reaches its peak.

Since you are trading patterns in implied volatility you want to have a high vega (in absolute value) but at the same time you don’t want to have any exposure on the underlying. In fact, if vega, which is the sensitivity of option prices to implied volatility, is low, even though the implied volatility moves as you expected you don’t make any profit because the value of your position is not sensitive to changes in the implied volatility. Moreover, you don’t want any exposure to the underlying because its price will move up or down depending on the outcome of the match and, given the uncertainty of the result, you don’t want to bet on it. So, you want your position to have a delta, which is the sensitivity of option prices to the price of the underlying, as close as possible to zero.

You can meet both the requirements of high vega and delta neutrality using at the money options. Indeed, both call and put options have a maximum vega when they are at the money. So, using at the money straddles will give you large positive vega for long straddles and large negative vega for short ones.  As for delta, theoretically at the money call and put options have the same delta but with opposite signs (positive for call and negative for put). Therefore, buying or selling at the money calls and puts as you do respectively in long and short straddles will give you a delta equal to zero at the opening of the position.

The main problem of short straddles is that you are gamma negative. Gamma is the sensitivity of delta to the price of the underlying. When you buy call and put options you have a positive gamma while when you sell calls and put, as in a short straddle, you are gamma negative.
Since our position has zero delta and it is held just for one day (theta is not too relevant), the profit or loss you make basically depends only on gamma and vega (see the formula below).

\Delta Value \cong Vega \cdot \Delta Implied \, Vol + \tfrac{1}{2} \cdot Gamma \cdot \left( \Delta Price_{Underlying} \right)^2

Since when you use short straddles you are gamma negative, you may lose money if the price of the underlying experience large moves, which is quite likely as we have shown in the event study. Therefore, the risk you run using short straddles is that if on the day after the match the stock experiences a significant move the loss due to the negative gamma could be larger than the gain coming from the decrease in the implied volatility.
In fact, Gao, Chao and Xing, Yuhang and Zhang, Xiaoyan (2017) show that selling straddles earns significant negative returns during earnings announcement periods. This result implies that, on average, implied volatility on options before earnings announcements is not large enough to compensate option sellers for the large price movements realized by stocks on the back of earnings surprise.
The long straddle can solve this problem because by buying call and put options you get a positive gamma, therefore if the underlying experiences large price moves, this will increase the overall profit of the position.

3.3 Empirical Results
As we did for the event study we backtested the long and short straddle strategies using data of Juventus Football Club and we considered only matches in the knockout stage of UCL. However, in this case we considered both victories and defeats.
Unfortunately, options on Juventus started trading only in November 2017, therefore we have a limited sample to analyze. Since November 2017 Juventus played six matches in the knockout stage of UCL. They are indicated in the table below:

For each date in our historical data, we had call and put options with several different maturities. We decided to remove options with maturity lower or equal to 14 days because of the traditional price distortions of options close to expiry. Among the remaining, we picked for each trade options with the second shortest maturity in that day. We made this choice, trying to pick options with medium maturities because on one hand implied volatility of too short-term options tends to be too volatile and can alter our results and on the other hand, long-term options appear to be not very liquid. As a result, we used options which have an average maturity of about 148 days.
We backtested two strategies: the first is a short straddle which is opened the day before the match and closed on the match day while the second is a long straddle which is opened on the match day and closed the day after. In both cases, we used the options with moneyness as close as possible to 100%, which are those closest to be at the money. The results of these two strategies for the six matches in our sample are summarized in the two tables below:

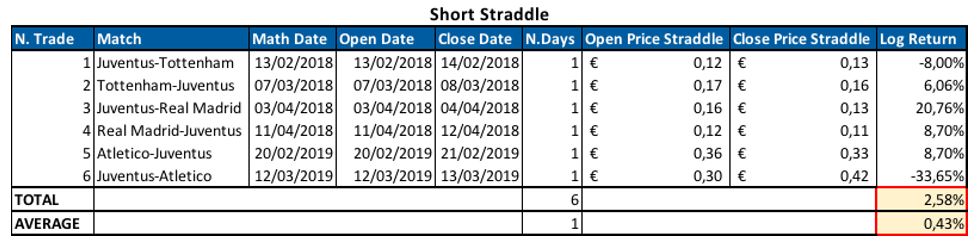
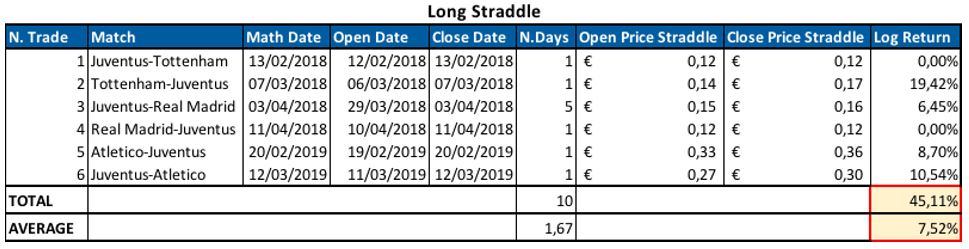
One complication could arise when computing the return of a short straddle position, since it is a credit trade, i.e. when we set up the short straddle we receive money. We compute short straddle returns as the opposite of the returns of a long straddle position. In other words, we considered the premia collected as the invested capital. This assumption is reasonable since option sellers have to post a margin to cover for the potential losses of their position.

The first table shows that shorting straddles is a positive return strategy in 4 events out of 6. Losses occur in three circumstances, two of them are the aforementioned exceptions to the pattern of implied volatility. As mentioned in the previous section, in Juventus-Tottenham of 13/02/2018 implied volatility does not spike pre-match while in Juventus-Atletico Madrid of 12/03/2019 implied volatility does spike before the match but it increases thereafter instead of dropping. Moreover, after that event, Juventus stock jumped for the unexpected qualification to the quarter finals, recording a stunning daily return of +17% (intraday Juventus stock traded also at +30%). The short straddle position was hurt by both the unexpected movement of implied volatility (we are vega negative) and the large price movement (we are gamma negative).

Since negative gamma is the greatest problem of the short straddle, we tested also a short strangle strategy. We build a short strangle by selling a call and a put with different strike prices. We consider 5% and 10% out-of-the-money options. Strangles have the benefit of a lower exposure to gamma, which could help reducing losses coming from large stock price movements after the match. On the flip side, however, they have a lower vega and premia collected is lower, since we are shorting out-of-the-money options. The returns of a short strangle strategy were equivalent to those of a short straddle from a qualitative perspective: the sign of the return of both strategies is the same for every event.

As you can see in the second table, buying straddle had given positive log return on 4 out of 6 trades. In the remaining two trades instead the return was zero because the price of put and call options didn’t move, probably because of too low liquidity.

Finally, we need to mention that in our analysis we didn’t consider transaction costs such as bid-ask spreads, which for single stock options, that typically are not very liquid, could be significant.

4. Arbitrage with Sport Bets

So far, we focused on trading UCL matches of the knockout phase using options on stocks of listed teams. However, we could use instruments other than options, such as sports bets. Sports betting, in fact, is by far the most popular and user-friendly tool available to people who want to “trade” football matches. In this section, we will explore whether we can arbitrage the two markets.

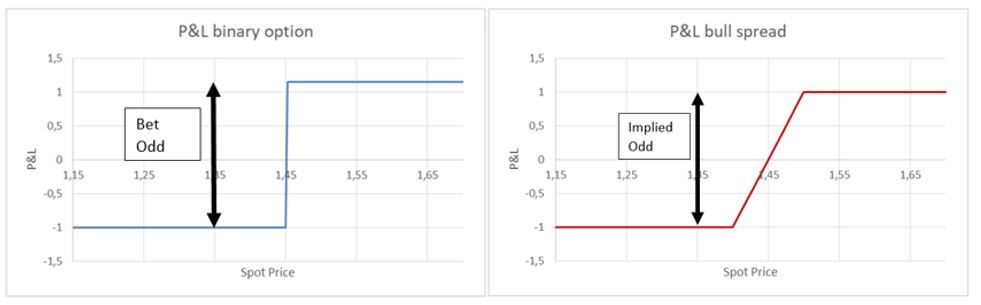
As a first step, we introduce sports betting. In particular, we focus on fixed odd betting, which is the most popular sports bet in Europe. In fixed odd betting, the bettor places a wager on the outcome of an event, such as a football match. The bookmaker acts as counterparty, setting the odds for each outcome so that the odds are known at the time of the placement of the bet. Odds can be expressed in different ways. The format we will use here is the EU format, also known as decimal odds. The figure quoted is the winning amount that would be paid out to the bettor by the bookmaker if he bets a unitary stake (EUR 1 betting stake).

The payoff of fixed odd bets resembles the one of a binary option. Binary options are derivatives in which the buyer receives a fixed payoff if the option expires in-the-money, i.e. if the price of the underlying is above the binary option’s strike price. However, this similarity is only apparent because binary options are derivatives and as such they have an underlying (e.g. Juventus stock). Sports bets, instead, apparently have no underlying. Nevertheless, it seems reasonable to assume that the bet of Juventus winning a UCL match of the knockout stage can be interpreted as a binary option with Juventus stock as underlying and with strike price equal to the stock price before the match. In fact, after the match, we expect the stock price to rise if the team wins and fall if the team loses. Clearly, the outcome of a football match is not binary because we also have the draw. For the sake of simplicity, we will consider the draw as a negative outcome, expecting the stock price to fall thereafter. This assumption is backed by the behavior of Juventus stock analyzed in the event study.

At this point, we want to use options on Juventus stock to replicate the payoff of the binary option, aka sports bet. To do so, we use bull call spreads. We could use a bull put spread too, but the bull call spread is better for our purposes as it is a debit trade (we pay to set up this strategy). We build a bull call spread by longing and shorting two calls with different strike prices: we long the low strike call and short the high strike one. We can theoretically replicate the payoff of a binary option with strike price K using a bull call spread in which we long 1/ε calls with strike K-ε and short 1/ε calls with strike K+ε, with ε→0. In so doing, the payoff of the bull spread can be made arbitrarily close to the binary option payoff by moving the strike of the short call as close as possible to the strike of the long call and trading a large number of contracts (1/ε→∞ with ε→0). Essentially, we are stretching the payoff of the bull spread to approximate the one of the sports bet. Clearly this replicating strategy is not perfect and practitioners usually set ε so that the replicating strategy is correct within a certain probability: P(K-ε < S < K+ε)< 1-α. Implementing this procedure in practice is challenging. Options traded in regulated markets are available for a limited number of strike prices, so we cannot have ε→0. Moreover, trading an infinite number of option contracts is unfeasible. Nevertheless, we are satisfied even with this approximation.

At this point, we can derive the odd implied by the bull call spread payoff. To do so, we simply notice that we can read the odd of the sports bet from its payoff diagram. The bet odd is the vertical difference between the payoff of the bet in the positive and in the negative outcomes. By the same token, we derive the odd for the outcome of Juventus winning the UCL match implied by the option market by normalizing the payoff of the bull call spread so that we get a loss of -1 in the worst scenarios (stock price below the lowest strike price). At this point, the implied odd is the vertical difference between the best and
the worst payoffs, i.e. the payoff in the best scenarios (spot price below the highest strike price) plus 1.

We implemented the procedure described above for the 6 Juventus matches in our sample. We built the bull call spread longing the at-the-money call and shorting the out-of-the-money call with the strike closest to the current stock price. We used option contracts with the shortest expiry, discarding options maturing within 14 days and considering in these cases option contracts at the next expiry date. We then computed odds implied by the bull spread and compared them with bookmaker odds for Juventus winning those matches. We took data on past odds from SportStats.com.

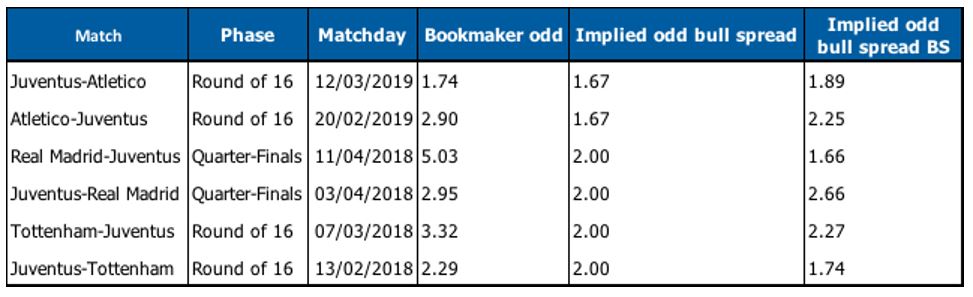
“Implied odd bull spread” are computed using actual option market prices, while “Implied odd bull spread BS” are computed using prices of options from Black and Scholes formula using as implied volatility the Rolling Implied Volatility index compiled by Bloomberg for at-the-money options derived from the end-of-day volatility surface. Market prices and prices computed with BS are identical if rounded at the first cent. As we can see, implied odds derived from option market prices are very stable across different matches, while implied odds derived from option priced from BS are much more volatile. This difference is mainly due to rounding: market prices of options from Bloomberg are rounded at the first cent.

We notice from the table that the bookmaker odd is always greater than the odd implied by the bull spread (the only exception is Juventus-Atletico Madrid, if we look at the odd implied by options valued with BS). Since we can replicate the payoff of the sports bet using bull spreads, we can create a (risky) arbitrage. On the matchday, we set up a bear call spread (i.e. shorting the bull call spread described above) and use the premia collected (as the bull call spread is a debit trade, the bear call spread is a credit trade) to bet on Juventus winning the match. We close the bear spread after the match. In doing so, we should gain an arbitrage profit as we are betting at the high bookmaker odd and financing our bet by selling a bull spread, which has an (almost) identical payoff but implies a lower odd for the same outcome. The arbitrage strategy proposed would have a 0 payoff if the outcome of the match is negative (Juventus loses or the match is a draw) as the loss on the bet is offset by the gain on the bear spread. On the flip side, the strategy will result in an arbitrage profit if the outcome of the match is positive (Juventus win), as we gain the higher bookmaker odd and pay the lower odd implied by the bull call spread.

The key risk associated with the strategy is that the bull spread does not replicate exactly the payoff of the binary option (the sports bet). This problem arises because of the limited strike prices available and the unfeasibility of trading an infinite number of contracts. However, the greatest issue derives from maturity mismatch. In fact, the binary option matures immediately after the match (when we cash the bet win) while options mature later. In our analysis, we used the option contracts closest to expiry (excluding those with maturity below 14 days) but the distortion introduced by time-value of options persists. We can understand the effect of this distortion by looking at the following graph (payoffs are scaled so that the maximum loss on the bet is -1 in order to facilitate the interpretation).

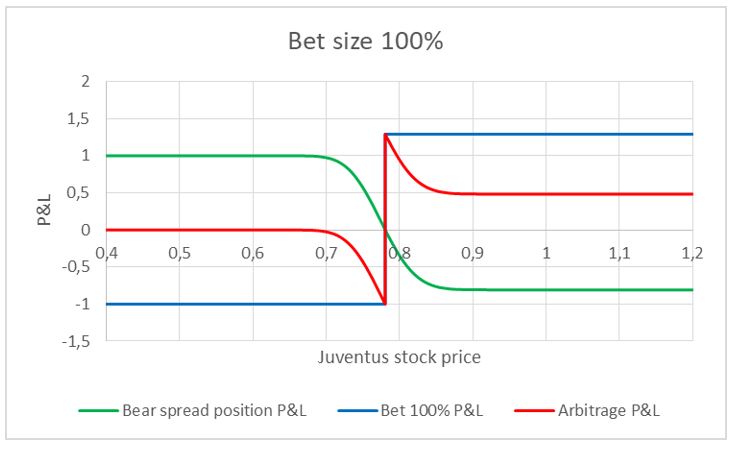
The red line represents the payoff of our arbitrage strategy. As we can see, for large price movements in either direction, the payoff is the one we would expect, but for intermediate price movements, time value distortions come into play. In particular, if the outcome of the match is negative and the stock price does not drop much, the gains on the bear spread do not make up for the loss of the bet stake. We could reduce the maximum drawdown and the minimum negative stock return so that the payoff of our strategy is not negative by betting a fraction of the premia collected on the bear spread. In other words, instead of betting 100% of the cash flows deriving from the bear spread, we bet only a fraction of it. This strategy will have the following payoff.

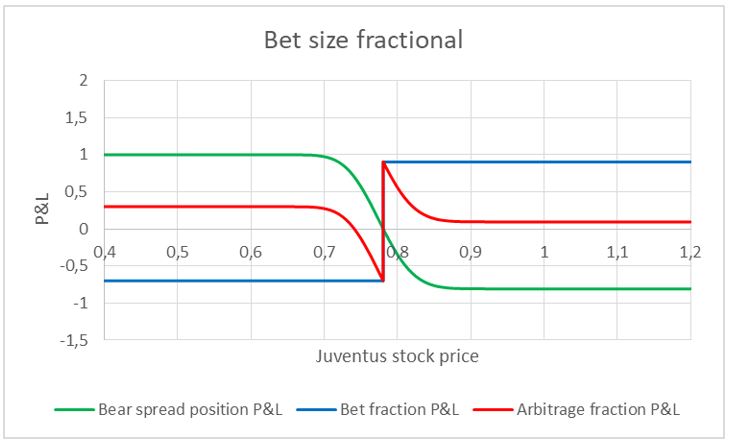
By decreasing the bet size, the payoff for negative outcomes becomes positive for large price movements as the payoff of the bear spread is larger than the bet size. Moreover, the payoff for positive outcomes is smaller because bet wins are only a fraction of the original ones. If the bet size is too small, we would end up losing money if the outcome is positive. We refer to this strategy as a risky arbitrage because for small negative price movements associated with a negative outcome, the strategy loses money. This is unavoidable.

In the following table, we report the returns of our risky arbitrage for the 6 Juventus matches of our sample, distinguishing between the case in which we bet 100% of the premia collected and the one in which we bet only a fraction of it (e.g. 40%). We compute returns considering as invested capital the premia collected when shorting the bear call spread. We trade 100 contracts each time.

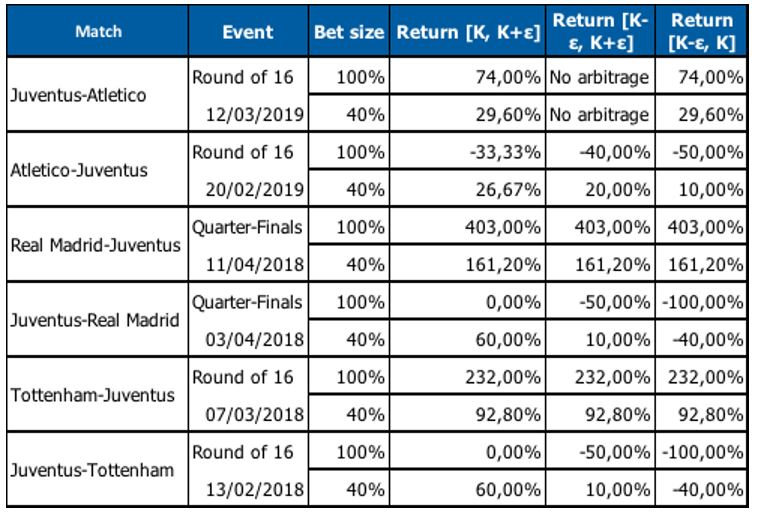
In the table, we reported the returns for the risky arbitrage strategy implemented with three possible choices of strike prices:

1. [K-ε, K+ε]: we use the in-the-money and the out-of-the-money options closer to the current stock price.
2. [K-ε, K]: we use the in-the-money option closer to the current stock price and the at-the-money contract.
3. [K,K+ε]: we use the at-the-money contract and the out-of-the-money option closer to the current stock price.

When returns are the same for the three column it is because a pure at-the-money option did not exist and so we used the same options for the three cases. We notice that betting 100% of the premia collected is a highly risky strategy, while a fractional bet size results in more stable returns. The best strategy uses [K,K+ε] as strike prices. In this case, the bear spread is more reactive to a negative return, resulting in a higher payoff, which offsets the loss of the bet stake.