A Primer on Equity Swaps

Download PDF

Introduction

The aim of this article is to provide a comprehensive overview of equity swaps, focusing on their structure, mechanics and use cases for investors. Equity swaps evolved in the late 1980s and early 1990s, as a part of the broader development of over the counter (OTC) derivative markets. They emerged to satisfy growing institutional investor demand for more sophisticated risk management tools and tailored financial products. Today, equity swaps are widely used, particularly for hedging purposes and managing large equity exposures. This paper will provide more clarity on equity swaps, including the players involved, valuations methods and how equity swaps compare to other derivate products in various use cases.

Undeniably, the most common equity swap structure are total return swaps (TRS) where one party receives the returns of the underlying equity/index in return for period payments to the counterparty. Another common equity swap structure are asset swaps, contracts between a financial institution and their clients to where both parties both receive equity returns, although on different underlying assets, and pay each other periodic payments. The structures will be discussed in the following sections proving an analysis on their structure, hedging strategies and their role in the financial markets.

Total return swaps

The widest spread swap in the equity word is the total return swap, used to gain synthetic exposure to the underlying asset. In a TRS, one side regularly pays a known rate (fixed or floating) plus a funding spread and receives the total return (all income +/- capital gain) of the underlying. The rate leg is known as “financing”, the other as “return”. TRS format therefore enables to gain exposure to financial instrument without actually owning it. This becomes very useful when access to the local market is restricted or when you don’t want to report your holdings. Thanks to this, TRS have become a popular tool for exposure access by many opportunistic players such as hedge funds and leverage-seeking investors.

Since a total return swap is an OTC product, it is not a standardized product and allows customizability in 1) the underlying 2) the notional of the swap 3) the expiration date 4) and rebalancing frequency. The underlying of a TRS can range from indices, futures, ETFs and single stocks. The notional needs to be agreed by both parties. Of course, the payment of the interest rate and performance of the underlying will be paid on the total notional (and is typically annualised), but the receiver of the swap will only put the upfront margin requirement (which is about 10% of the total notional). Lastly, the parties can agree whether the swap will be on term or on open. A term TRS has an expiration date, by which the parties are no longer obliged to follow the swap agreement, but if the TRS is open it means that until the buyer of the swap agreement doesn’t sell it back to the bank, the payer will still have the obligation to pay the performance to the third party. Lastly, TRS are market-to-market and depending on if the underlying goes up (down) the buyer of the swap will have to put less (more) collateral.

Suppose a hedge fund wants to gain synthetic exposure of XYZ stock, putting a much lower up-front payment vs buying the stock in the market. To do this, he will contact his prime broker and arrange the terms for a TRS. Once the terms are agreed, the hedge fund will have to pose the margin collateral and will start receiving the performance of the stock synthetically.

This is how the transaction looks like if no hedging is done by the bank and supposing an open swap. The PnL from the swap is calculated on a mark-to-market basis where each day additional collateral will be posed/withdrawn depending on the performance of this underlying. If the underlying appreciates 5%, then the bank (who is short TRS in this example), will have to pay the client 5% of the total notional amount of the swap (this will likely be collateral withdrawn from the client). Conversely, if the underlying depreciates 5%, the bank is entitled to receive 5% of the total notional from the client.

Hedging total return swaps – for the bank

You can see from the previous example how the bank is exposed both to interest rate risk and delta risk as the interest rate was locked in the moment of the agreement. This means that if the bank wants to keep delta risk, but hedge the interest rate risk, they would need to pay an interest rate swap.

To fully understand where the funding spread comes from, one would need to consider how the bank hedges delta and interest rates risk. Here is a real-life example of how banks would execute this position:

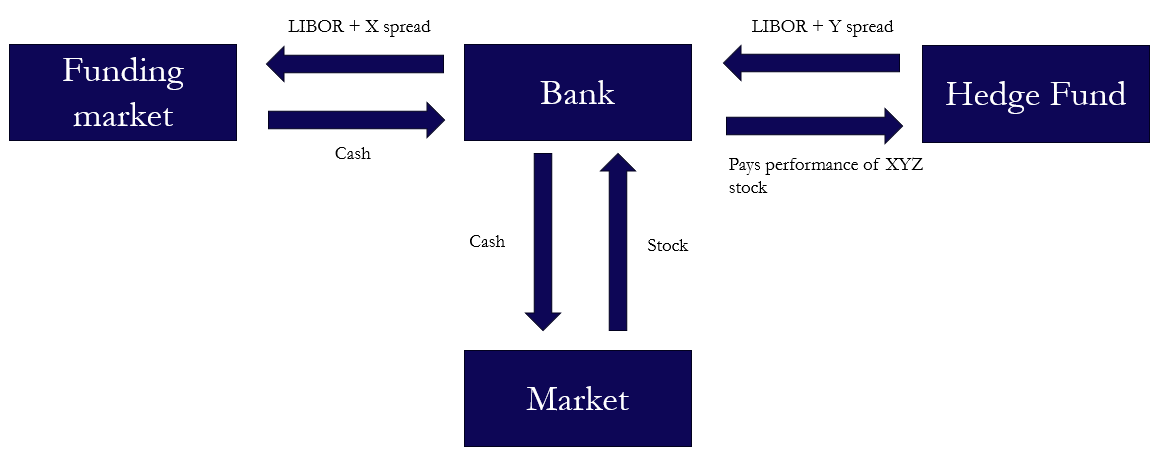
To delta hedge the bank needs the underlying asset (in the same notional amount) so that movements are offset by each other. If the bank is short (long) TRS, they will need to buy (sell) the stock. But where exactly does this money come from?

Since most banks have balance sheet constraints, they will need to raise cash in the funding market (treasury). The funding market will charge them a spread above the LIBOR rate called the funding spread, which will then be passed on the client as a Y spread. Basically, the rate that the client pays to receive the swap is the LIBOR + hedging costs. In fact, the Y spread also depends on other factors:

1. The underlying liquidity of the stock (the less liquid the higher the bank will charge as hedging becomes more difficult).
2. Volatility of the stock (the more volatile, the higher the spread will be).
3. Demand and supply for borrow and quality of the stock. There is a trade-off between holding physical vs synthetic exposure for the bank. If you hold physical inventory, you can lend the stocks to another party who is willing to short. This implies that you earn a lending fee for lending out the stocks. On the other hand, if lending fees are low, the opportunity cost of holding physical inventory is high, as it would be much cheaper to have the stock synthetically. This is why the quality of the stock matters: the higher the quality of the stock, the higher the lending fees might be, which lead to a higher spread as the banks need to be compensated to hold synthetic exposure (as it would be beneficial to hold the stock on the balance sheet and lend it out).
4. Demand and supply for funding. The funding market plays a crucial role in pricing a swap as the bank will rely on funding to raise the cash to hedge. For example, at the end of year, the Basel Committee requires a sample of banks to report a set of indicators to national supervisory authorities. These indicators are then aggregated and used to calculate the scores of banks in the sample. Banks above a cut-off score are identified as G-SIBs and are allocated to buckets that will be used to determine their higher loss absorbency requirement. If you are inserted in the lower end of the brackets, you will have to pose additional capital as a requirement. This means that banks will likely reduce balance sheet risk at the end of year to be placed in the higher end of the brackets. To do this, instead of holding physical inventories, banks will likely enter swap agreements. By doing so, demand for funding increases dramatically, making swaps more expensive.
5. Term vs open swap. If the swap in on an open agreement, it means that the predictability of the client is reduced, thus increasing uncertainty as the bank doesn’t have an idea for how long the hedge will be on their balance sheet. This means they will charge a premium.
6. Dividends. By using TRS, investors can effectively manage dividend payments as they receive the full economic benefit of the underlying asset, including any dividends. However, complications arise when the underlying is a future on an index/ETF. This is because indices can be 1) price return 2) gross total return 3) net total return. Therefore, the market maker needs to consider which is the underlying product.

Asset swaps

Balance sheet optimization for banks is essential, they will always face a balance sheet constraint and will therefore opt to hold the least amount of physical inventory, at least in normal times. When borrowing costs are high, physical inventory is beneficial because it allows the bank the optionality to lend out the shares (to a short seller) and earn an interest. But it a period of low borrowing costs, physical inventory might be very costly. Furthermore, not all banks are allowed to hold certain types of stocks (where there are access restrictions), but the performance of the restricted underlying wants to nevertheless be earned. Synthetical inventory is also beneficial as it allows for a cheaper hedging alternative. Therefore, there are occurrences where investment banks keep their inventory synthetically.

On the other hand of the spectrum, there are beta funds, whose aim will be to closely track an index and be able to outperform the benchmark. To do this, these types of funds will typically enter into yield enhancement strategies, like selling OTM calls on stocks they already earn to earn a slight premium. Another way these benchmark funds can yield enhance is by entering into an asset swap agreement with a bank.

An asset swap has a TRS incorporated in it but differs slightly in how it is used. Suppose a fund is tracking the performance of MSCI Word and is trying to yield enhance its portfolio and the bank is interested in gaining synthetic exposure in an underlying basket of stocks, to optimize the balance sheet/hedge positions/internalize liquidity.

The first leg of an equity asset swap will be a transaction between the client and the market, where the client sells the index and raises cash. Since the client is still trying to replicate the benchmark, the bank will sell them a TRS on the exact index that was sold (to replicate the exact performance), but in return the client will need to buy a basket of pre-determined stocks which the bank needs. These stocks are discretional on the bank, and the choice depends on hedging demand, axes and lending availability.

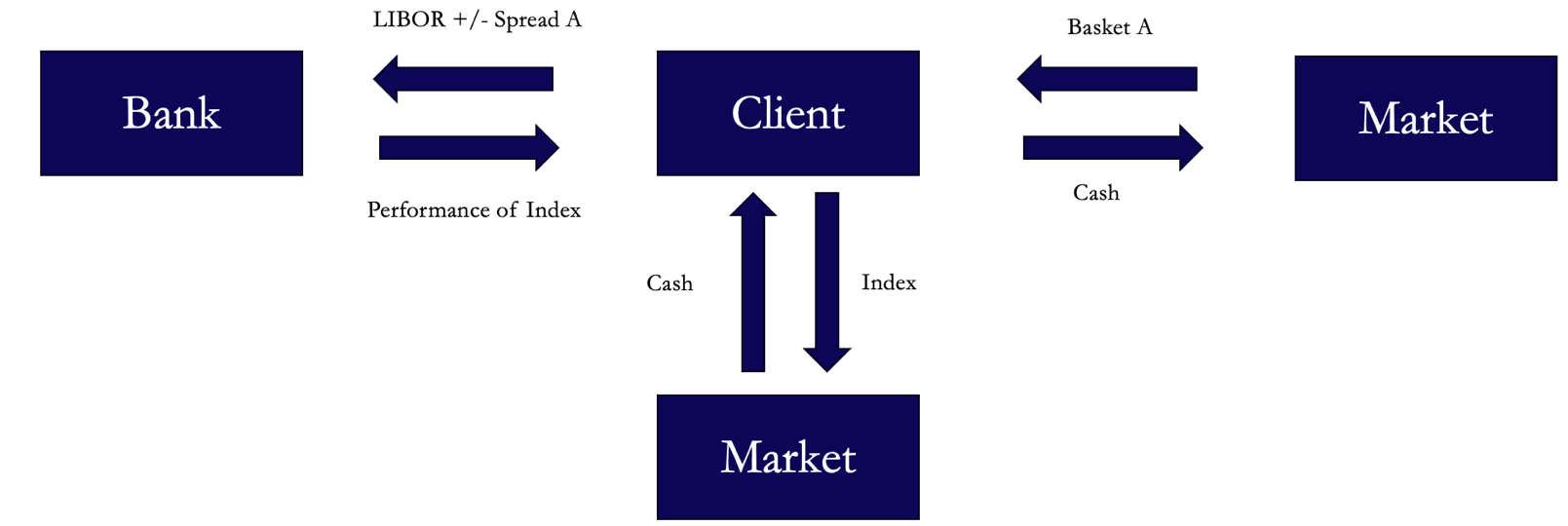
Once the client has bought the basket of stocks for the bank, the second leg of the asset swap begins, where the client pays the performance of the basket of stocks to the bank.

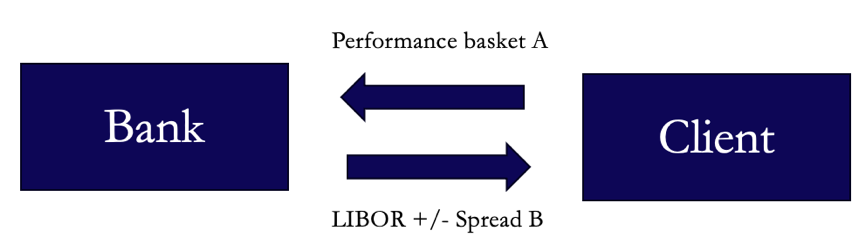
By doing so, both parties are receiving what they want: the bank is gaining the synthetic exposure to a basket of stock of their choice and the client is yield enhancing as typically Spread A < Spread B.

Advantages of Equity Swaps

The reduction in initial outlay is an apparent advantage of this type of financial instrument. Equity swaps enable investors to gain exposure to equity markets without the need for substantial upfront capital. The financing leg only requires a margin deposit rather than the full purchase prices of the equities, thus reducing the initial outlay for the return leg. It goes without saying that this allows for increased leverage, as it allows investors to the exposure of a notional amount of equities by posting a margin deposit to cover potential losses. If losses erode the margin deposit, the return leg may need to post additional funds, which may entail a close and constant inspection of the position due to the potential for rapid loss accumulation.

Nevertheless, equity swaps can reduce operational workloads and human capital requirements. Managing a portfolio of equities involves various operational tasks including settlement procedures, custody services corporate actions management and compliance with regulatory requirements. Equity swaps transfer many of these responsibilities to the counterparty (banks, in the examples detailed above). A concrete example of this advantage is the lack of obligation to disclose their holdings to regulatory authorities and the public, which is otherwise required when investors acquire significant positions in publicly traded companies. Because of the nature of equity swaps, the return leg gains economic exposure to equities without holding them directly, ultimately bypassing certain disclosure agreements.

Another logistical advantage of owning equity swaps compared to the underlying equities involves savings in taxes and custodian fees. In both the USA and the EU, equity swaps provide numerous tax advantages. Firstly, equity swaps allow investors to defer taxes on gains, improving cash flow and investment compounding potential. Equity swaps also allow for dividend tax efficiency, replicating dividend exposure without incurring immediate dividend taxation or withholding taxes. Additionally, equity swaps may benefit from flexible tax treatment, for example reporting gains as financial income instead of capital gains. Finally, equity swaps may not trigger rules such as was sales, allowing for strategic realization of losses.

Finally, as anticipated towards the beginning of the paper, equity swaps provide access to restricted markets to foreign investors. Some equity markets impose restrictions on foreign investors, limiting their ability to buy shared directly. Equity swaps provide synthetic exposure to such markets, allowing investors to receive returns based on the performance of the underlying equities without holding them. An apparent and relevant example of this is China’s regulations on its A-shares, shares issued by Chinese companies incorporated in China, listed on the domestic stock market and open to investors. On these shares, Chinese regulators have imposed a 10% individual limit, meaning that a single foreign investor is not allowed to hold more than 10% of the total outstanding shares of any A-share listed company and must comply with disclosure obligations if their holdings reach 5% of total shares outstanding. Naturally, because of the synthetic exposure provided by equity swaps, these restrictions can be averted.

Pricing and Valuing of TRS Equity Swaps

In equity swaps, pricing refers to individuating the financing rate paid by the return leg, which allows the transaction to mimic the cost of funding a leverage position in the equity and imposes a market value of 0 at the swap’s inception. As will be explored later in the article, the returns profile for a leveraged equity position and an equity swap of the name notional value differs, but mimicking the cost of funding a leverage position plays a key role in pricing this asset class.

The process of pricing an equity is the following:

Consider a swap where the return leg pays a fixed rate of R to the financing leg. Firstly, we can summarize the swap’s first cash flow and cashflows for any time like so:

Now, the objective is to find a trading strategy that replicates the swap’s cashflows. This strategy consists of a series of transactions consisting of opening a position on the equity and subtracting 1 plus the rate. Let us consider the first payment, the cashflows can be replicated by:

At time j:

1. Investing the amount 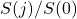in the stock
2. Borrowing

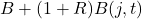
Where B is the price of a 0-coupon bond at time j, which is set to pay 1$ at expiration to increase workability.

At time t, the following occurs, the stock will be worth:

On paying off bonds for a value of , the total cashflow is:

This process is equivalent for all cashflows, the stock is purchased at time j and funds are invested in the risk-free asset to mature to a value of 1$ one period prior to the date of the cashflow that is being replicated, then that 1$ is invested in stock. Also, at time j, funds are borrowed to be paid back in the amount of at the time of the swap payment. This allows us to calculate the total value of these transactions at j as:

This formula allows to calculate the market value of a swap in any time j. In this example, the swap was created at time 0 and the next payment is the first one. This does not have to be the case, without loss of generality we can let time 0 be the last date in which a payment was made or swap initiation date, whichever is more recent, and be the number of upcoming payments. Noting that the first term of the formula simplifies to 1, we set the market value to 0. Now that we have the market value formula and the market value of the swap is set to 0, we can solve for R and price the swap like so:

The process for the pricing and valuation of an equity swap where the return leg pays a floating interest rate to the financing leg is similar but worth overviewing.

In this scenario, the swap can be replicated by opening two positions being: a) a swap to pay fixed and receive equity + b) a swap to pay floating and receive fixed. Notice that swap a) has an identical structure to the swap priced above, whereas swap b) is a plain vanilla interest rate swap, the value of which is:

Where is the one-period floating rate that was observed at time 0 and determines the next payment. Adding the values of swaps a) and b) and simplifying we obtain the value of the pay floating, receive equity swap as the following:

Intuitively, there is not pricing of this swap as it has no fixed rate. It is necessary however to verify that the value is 0 at time j = 0 as otherwise it would allow for arbitrage opportunities as one leg would be intrinsically more valuable than the other. To verify that the value of the swap is 0 at time j = 0 we first set j to 0 in the above equation and obtain the following:

By definition, . Hence, the value of the swap is zero at the start.

Conclusion

In summary, since their inception in the 1980’s equity swaps have become a core tool in equity investing, managing financial institutions’ balance sheets and risk profile, and accessing restricted markets. Their flexibility allows institutional investors to create ad hoc instruments to satisfy their needs without sacrificing excessive human capital or returns.

Despite their prominent use for the last forty years, new regulatory protocols have been put in place and are being drafted to increase efficiency and transparency when trading equity swaps. The most recent protocol being the ISDA 2023 Equity Swap protocol which introduced streamlined terms and the ability to incorporate updates automatically without needing individual supplements. These changes make swap documentation more efficient and adaptable to evolving market practices and regulatory changes.

As equity swaps continue to evolve and integrate with new technologies and regulatory frameworks, they are poised to play an even more significant role in offering investors flexible, efficient, and tailored exposure to a wide range of global markets, bridging the gap between traditional and alternative investment strategies while enhancing risk management and capital efficiency across the financial ecosystem.

References

1. Norton Rose Fulbright, “An overview of the ISDA 2023 Equity Swap -2021 definitions Protocol”, 2023
2. Don M. Chance, “Equity swaps and equity investing”, 2003
3. Hedgeweek, “Equity swaps as an alternative to trading in equities”, 2005
4. BIS, “Global systemically important banks: assessment methodology and the additional loss absorbency requirement”, 2023