Introduction
Credit Default Swaps (CDSs) have had an interesting trajectory to say the least, starting out as a niche derivative, they rose to prominence after the Russian financial crisis of 1998, ballooning into a market worth an enormous $62.2 trillion in 2007. In 2008, this market promptly collapsed, producing a mushroom cloud worthy of Warren Buffet’s designation of CDSs as ‘financial weapons of mass destruction.’ However, the CDS market is far from finished, standing at $8.8 trillion in the first half of 2020 according to the Bank for International Settlements.
In this article we’ll give a quick primer on the theory underpinning these derivatives and explore CDS indices and their arbitrage, curve trades, and the relationship between credit risk and equity volatility, proposing a pairs trade.
What are Credit Default Swaps and how do they work?
Credit Default Swaps are over the counter financial contracts that allow investors to regulate their exposure to credit risk. While the most straightforward use of credit derivatives is to hedge the risk derived from investing in bonds or other credit securities, they are also used to express views on the creditworthiness of one or more entities (i.e., the governments or corporations who issue the bonds.) Beyond taking a simple directional bet in the form of buying/selling a single-name CDS, investors can express their view on the relative value of two different credits (pairs trading), the time when an entity will default (curve trading), the capital structure of the entity etc.
The terms of a CDS contract dictate that, until maturity (usually five years), the protection buyer must pay a periodic fee to the protection seller, who agrees to cover the losses on the underlying if a credit event happens; credit risk is ‘swapped’. Typical credit events include bankruptcy, debt restructuring, obligation acceleration and failure to pay.
The protection seller profits from the periodic payment made by the buyer, given a credit event doesn’t occur. The market price of the CDS, the spread, gives the percentage of the notional value of the contract payed per year. The notional is defined as the maximum amount that the seller will pay in case of default. It is important to note that while the spread is the percentage paid per year, the buyer usually makes quarterly payments amounting to the notional times 25% of the spread. In effect, a CDS contract can be uniquely defined by four parameters: reference entity, notional, spread and maturity.
How does settlement take place?
If a credit event occurs, the amount paid by the seller is the notional multiplied by (1 – the recovery rate). The recovery rate is the market value of the underlying as a proportion of the par value, after the credit event (at the time the CDS is settled.) The buyer is also obligated to pay the seller the spread that has accrued from the last periodic fee until the date of the credit event.
Physical settlement is when the protection seller buys the defaulted bonds from the buyer at par value. This works well when CDSs are used as a hedge, however, since CDSs are frequently used for speculation (in fact their trade volume exceeds the number of underlying securities), another method is often used, namely cash settlement. With cash settlement, the CDS seller simply pays cash equal to the devaluation of the security as described above. For example, say a bond was initially worth $100 and its market price at the date of the credit event is $25. The CDS seller will pay the buyer $100 – $25 = $75 for every bond. In summary, either way, the seller pays out all the value which is not recovered, effectively neutralizing credit risk for the buyer.
Finally, out of the need for a more transparent form of settlement after the global financial crisis and to reduce the net cash flow from sellers to buyers, credit event auctions were developed. These grant investors the possibility to choose between physical and cash settlement and establish one price for the whole market and assign the same recovery rate to all the reference entity’s debt obligations of the same seniority. These auctions consist of two stages. In the first stage, dealers post bid and ask prices for the bonds given the spread, determining a starting point for the recovery rate, called the inside market mid-point. Then, the size and direction of open interest (net of buy and sell positions) is determined. If open interest is zero, the inside market mid-point is the official recovery price. Otherwise, participants have three hours to send limit orders, which are buy orders if open interest is to sell and sell orders if open interest is to buy. At the second stage, a price is determined to match open interest to limit orders, thus eliminating excess supply/demand and setting the official recovery price.
It is important to note that CDS investors can (and often do) close their positions in the absence of a credit event to lock in profits arising from the spread widening (if the investor is a protection buyer) or tightening (if the investor is a protection seller.) The spread on CDSs widens or tightens when market participants perceive credit risk to have increased or decreased. Imagine an investor has bought protection on an investment grade bond for 50bp. All of a sudden, macroeconomic conditions become extremely adverse and drastically impact the reference entity’s business. Spreads on CDSs will then widen significantly, say to 250bp. The investor can then unwind them (sell the contracts to someone else), receiving the present value of future payments, namely 250bp-50bp=200bp times the notional times the probability that the company does not default, for the remaining time to maturity.

CDS indices
Credit default swap indices are tradable products that allow investors to take long or short credit risk positions in specific credit markets or segments thereof. CDS indices reflect the performance of a basket of securities, more specifically single-name CDSs (contracts on an individual reference entity) and have fixed composition and maturities. Just like instruments derived from the S&P 500 or the Dow Jones, CDS indices are tradable and they can be used to write derivatives. Note that, in the event of a default of one of the underlying reference entities in the index, the investor receives a payment proportional to the weight of the defaulted entity in the index and the principal value of the note decreases to account for the default.
CDS indices were introduced in 2003, when J.P. Morgan and Morgan Stanley launched an index known as Trac-X. The product was a development on the two bank’s preceding synthetic tracers, which were tradable baskets of investment grade CDSs. Soon after that, some American and European banks joined forces to launch an index by the name of iBoxx, and when iBoxx merged with Trac-X, in 2004, the famous iTraxx was born. iTraxx is equal-weighted and offers indices based on European, Asian and emerging markets credit. Another very important CDS index is CDX which offers indices based on both North American and emerging markets credit. Both are operated by Markit and offer exposure to a range of securities from investment-grade to high-yield.
CDS indices have expanded remarkably in the past few years leading to increased trade volume, lower trading costs and enhanced visibility across markets. This is because indices are more easily traded than baskets of cash bond indices or single-name CDSs and they entail lower transaction costs and are more liquid. Finally, there is greater transparency and industry support.

CDX-CDS Arbitrage
The CDX-CDS basis is the absolute value of the difference between the spread on the CDX index and the spread implied by the spreads paid on the replicating portfolio of single-name CDSs. In this trade, the arbitrageur receives the difference between the index spread and the equal weighted spreads on the underlying single name CDSs, net of the funding cost of the initial and variation margins required for each CDS contract purchased and sold.
Though they don’t always exceed transaction costs, opportunities to profit on the basis between the prices of CDX and the underlying single names do exist. Due to the tighter bid-ask spread on CDX compared to CDSs (because of CDX’s standardization and higher liquidity), purchasing relatively cheaper CDX and selling the underlying CDSs seems like the more likely opportunity (rather than buying CDSs and selling CDX.) This trade generates P&L at inception and is considered to be default-risk-free as the portfolio of single name contracts perfectly replicates the payoffs from the index contract.
However, it is important to consider that there is always the risk of a double default, where both the firm underlying the CDS and the counterparty to the CDS default, and since it is mandatory that CDX contracts be centrally cleared, while single name CDS contracts are cleared on a voluntary basis, the margin requirements for the long and the short sides of the CDX-CDS trades cannot be offset against each other (only about 40 percent of the single name contracts underlying the investment grade index are eligible for central clearing.) Additionally, all 126 single name contracts necessary for this trade will have non-zero upfront payments, increasing trade cost. Finally, as with any trade involving CDX, it is important to consider that whenever the index rolls, the newly off-the-run index becomes far less liquid.
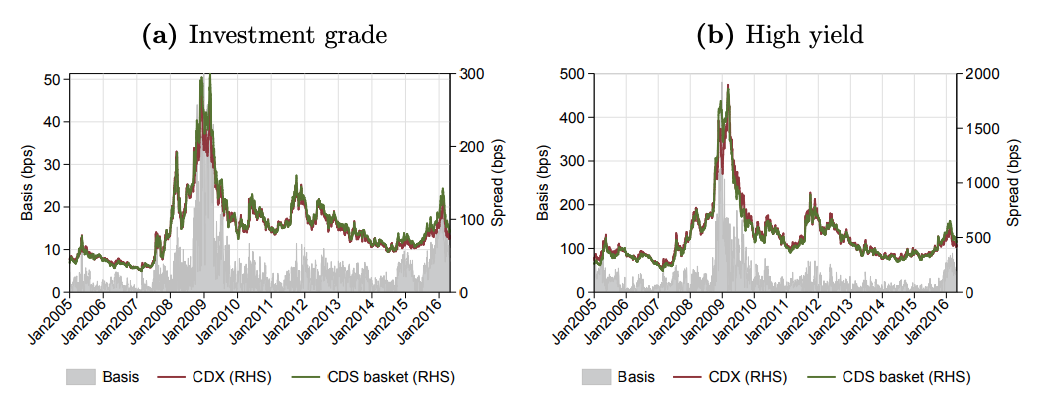
Figure 1. Historical evolution of the CDS-CDX basis. Source: Markit
Credit Curves
The spread demanded for buying or selling protection on a reference entity’s credit varies with the length of the period for which protection is sought. A credit curve is a set of points indicating the spread on a CDS for different maturities. Each point belonging to the curve represents the spread that makes the present value of expected spread payments is equal to the present value of the payout in case of a credit event (fair pricing.) In other words, it makes the present value of the Fee Leg (protection buyer) is equal to that of the Contingent Leg (protection seller.) We’ll quickly delve into what the slope of the curve indicates about market sentiment before discussing curve trading.
To understand the slope of credit curves we first need to introduce the concept of hazard rate. The hazard rate is defined as the conditional probability of default in a specific period and it is denoted by ![]() , t being the period under consideration. Symmetrically, probabilities of survival are defined as
, t being the period under consideration. Symmetrically, probabilities of survival are defined as ![]() . When credit curves are upward sloping, what is increasing over time is not the probability of default for the credit in question but the hazard rate, this means that the probability of default in any period (assuming the reference entity has not defaulted up until then) increases with time. Therefore, markets are not only implying that default becomes more likely with the passage of time, but also that the rate at which the probability increases is increasing itself (in other words, a positive second derivative.) Thus, creditworthiness decreases as we move from one period into the next. Upward sloping curves are typical of investment grade companies, which are considered unlikely to default in the short term but still require wider spreads to account for the inherent uncertainty corresponding to longer maturities.
. When credit curves are upward sloping, what is increasing over time is not the probability of default for the credit in question but the hazard rate, this means that the probability of default in any period (assuming the reference entity has not defaulted up until then) increases with time. Therefore, markets are not only implying that default becomes more likely with the passage of time, but also that the rate at which the probability increases is increasing itself (in other words, a positive second derivative.) Thus, creditworthiness decreases as we move from one period into the next. Upward sloping curves are typical of investment grade companies, which are considered unlikely to default in the short term but still require wider spreads to account for the inherent uncertainty corresponding to longer maturities.
A flat curve indicates that although a credit event is considered likely, there is uncertainty as to when it will occur. Finally, downward sloping credit curves are typically associated with companies that are expected to default in the short term because they indicate high hazard rates (i.e., low probability of survival) in the short term, suggesting investors believe they won’t survive the coming months, but lower hazard rates as we move into the future, the rationale being that after the tough period ends, the entity will be relatively less likely to default and may be more resilient than expected.
Trading Credit Curves
The main reason an investor would be interested in trading curves instead of single points is that they may not be sure about which point will move but they wish to express their view on the relative steepness of the curve (a.k.a. the ‘term structure’ of credit risk.) Additionally, by trading a curve, the investor doesn’t have to take the exposure associated with taking a position on the possibility of a credit event by a specific maturity.
Curve trades are divided into two main categories: curve flatteners and curve steepeners. A curve flattener is a bearish trade where the investor expects that the credit curve will become flatter, and thus buys short term CDSs and sells longer term ones. Conversely, a curve steepener is a bullish trade executed by an investor who seeks to express an optimistic view on an entity’s creditworthiness and thus sells short-term while buying longer term.
The majority of curve trades are implemented using DV01-neutral weighting. DV01 indicates the dollar value change in the present value of a CDS for a 1bp change in the spread. Basically, the DV01 associated with a CDS represents the duration of the position, because it can be interpreted as the present value of receiving 1bp every year until maturity. Moreover, a DV01-neutral CDS position is analogous to a duration-neutral bond position.
To compute the DV01 we discount the stream of 1bp payments using two discount factors: the risk-free rate and the probability of survival, which we’ve defined above. To execute a DV01-neutral trade, the investor needs to buy and sell on two positions on the curve such that their combined notionals amount to zero. Suppose we are interested in a 5s10s steepener trade (selling 5yr CDSs and buying 10yr ones). A DV01-neutral trade would require selling 5yr notional equal to:
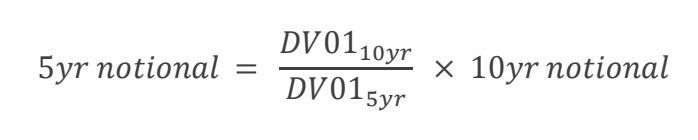
The reason DV01-neutral trades are so popular is rather straightforward: they are not affected by shifts in credit curves, i.e., virtually no mark-to-market change when spreads on all maturities move in the same direction by the same amount. The trade is only affected by changes in slope and is protected from moves that impact the whole market, assuming spreads move in parallel.
We can now move on to a very concise overview of some of the factors affecting curve trade P&L. As you might expect, the most relevant one is a change in the slope of the curve. In fact, for DV01-neutral trades, the P&L is proportional to the absolute slope. When an investor enters a curve steepener/(flattener) trade, they profit from the absolute slope increasing/(decreasing.) If no change in slope occurs, the P&L is given by adding the carry and the roll-down. Carry being the net premium paid (if you’re a buyer) or received (if you’re a seller) and roll-down being the change in the value of the CDSs (due to the passing of time) assuming the curve is unchanged until maturity or default.
Finally, the convexity of the trade describes the amount of change in DV01 resulting from a change in spread. Such a change can cause the position to become over or under-hedged. The DV01 decreases when the spread increases, because a spread increase indicates a higher probability of default and thus a higher discount rate, and vice versa. Curve flatteners have positive convexity, losses arising from a steepening are softened and gains from a flattening boosted, whereas curve steepeners have negative convexity (concavity), that is, losses from a flattening are intensified and gains from a steepening are dampened.
The Relationship Between Credit Spreads and Equity Volatility
There’s an intuitive link between volatility and credit risk: higher volatility generally indicates a tumultuous market, which would naturally lead us to expect higher default risk on outstanding debt. This relationship is somewhat affirmed when we consider that the most well-known credit risk model, the Merton model, takes into account firms’ stock price and volatility. However, questions remain: empirically, does volatility induce credit spreads to widen or is it the other way around? How can we profit from their relationship? To answer both of these questions, we’ll analyze price discovery for the VIX and the 47 most liquid iTraxx companies, relying on insights from Isabel Figuerola-Ferretti and Ioannis Paraskevopoulos’ paper “The dynamic relation between CDS markets and the VIX index.” [1]

At a glance, the above chart shows the VIX and credit spreads tracking, but as a precursor to answering the questions we’ve posed, we must ensure that a statistical relationship does indeed exist between them. Let xt be the price of a credit derivative at time t and vt be the contemporaneous price of a derivative written on the VIX. By examining daily Bloomberg data for the VIX and 3-, 5- and 10-year maturity iTraxx indices between June 2004 and December 2009, Ferreti and Paraskevopoulos find that xt and vt are clearly cointegrated, meaning that they are correlated and cannot deviate from equilibrium in the long term (if the analysis is correct, of course), setting us up for a Boaz Weinstein-flavored relative-value/mean-reversion trade we’ll come back to later. The analysis can be interpreted as estimating the Vega sensitivity of a credit portfolio (P). When the credit portfolio is the 5-year iTraxx:
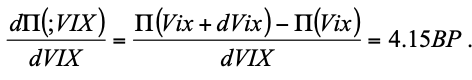
Meaning if volatility goes up by 1 bp, the cost of insuring a credit portfolio will go up by 4.15 bps on average.
Now onto price discovery and the answers to our original questions.
There are two popular common factor metrics that are used to investigate the mechanics of price discovery, but both begin by the estimation of the following Vector Error Correction Model (VECM):
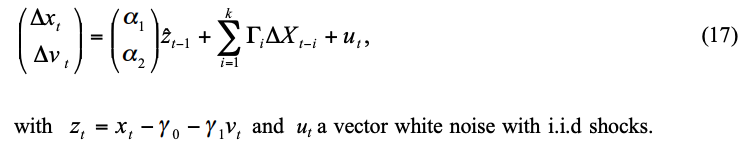
In this VECM, zt-1 is the long-term relationship that governs both variables and its adjustment coefficient or adjustment vector describes how the VIX and iTraxx react to deviations from the long-term equilibrium. The adjustment vector gives us the answer to our first question; if the CDS market contributes significantly to price discovery, α2 will be positive and statistically significant, while if the VIX derivative market contributes significantly, α1 will be negative and significant. If both are significant, then both markets contribute to price discovery.
If a given shock to the long-term relationship makes zt-1 > 0 this implies that iTraxx will have to drop and/or the VIX will have to increase to restore equilibrium (if zt-1 < 0 the opposite is required.) The same applies to individual CDSs. Interestingly, the data shows that the VIX index does not react significantly to equilibrium error, whereas the iTraxx index does, meaning that the VIX dominates iTraxx in terms of price discovery. On average, if there’s disequilibrium, it is the credit derivatives market which does the adjustment, not the volatility derivatives market. This result is independent of the iTraxx maturity chosen (though it is stronger for the 3- and 5-year case) and is confirmed by the price discovery results between VIX an individual CDSs; in 36 of the 39 companies analyzed, α1 is significant, indicating that the VIX market contributes to price discovery while the CDS market (α2) only appears to have a significant role in 9 out of the 39 cases. The VIX leads the CDS market.
This calls for pairs trading: open a long-short position when the paired prices have diverged by a certain amount and close the position when they revert. When VIX and Itraxx deviate from their long-run relationship, we short the out-performer and go long the underperformer, hoping they’ll converge back. This strategy is typically market neutral; if the market goes down, we lose from the long and gain from the short, and vice versa. In theory it is also a zero cost strategy as we can use the proceeds from the short position to finance the long position. Having said that, it is not risk-free: when the VIX and CDSs drift away from each other/their long run relationship, we incur a loss. The following table reports average daily excess returns and annualized Sharpe Ratios from the pairs strategy vs. investing in VIX or iTraxx alone, showing improved absolute and risk-adjusted performance:

We would be remiss if we did not include a few caveats, however. First of all, the data examined in this paper is almost 10 years old, and precisely which VIX derivatives are being considered is never specified. Additionally, the model assumes there are no transaction costs and looks at iTraxx when the more sensible choice seems to be CDX.NA.IG, considering the VIX measures S&P volatility a.k.a. the volatility of North American (rather than European), investment-grade firms’ stock.
Interestingly, recent months have presented the largest VIX-CDX pairs trade opportunity in 20 years, though an ISDA is needed to take advantage of it. According to Bloomberg, CDS veteran Boaz Weinstein “hasn’t seen such a disconnect between the complacency of credit investors and the anxiety of equity investors” in his 22-year career; October 22nd, 2020:

The Bloomberg article sheds some light on what Weinstein brings to the trade beyond recognising the statistical anomaly, a sound understanding of the economic and financial reality underpinning (or not underpinning) market moves. This allows him to better position himself to profit, and profit he has; his hedge fund, Saba Capital, pulled in a very sizable 33% gain to its Master Fund and a colossal 99% gain to its Tail Hedge Fund in March alone.
‘He [Weinstein] pounced on the divergence between the VIX and credit spreads. For years they moved in tandem, then in August the VIX started rising as spreads kept falling. With so many “known unknowns” — such as the election outcome, Covid-19 spread and the pace of the economic recovery — a high degree of implied volatility in equities makes sense, Weinstein said. The sanguine outlook for credit doesn’t, especially with yields low and defaults mounting. He’s shorting the credits he considers most vulnerable to a pullback, declining to name them, but also has long positions on issuers that “are going to be in good shape no matter what happens” including AT&T and the Walt Disney Co.’ [2]
References
[1] webs.ucm.es/info/icae/seminario/Figuerola_dic14.pdf
[2] bloomberg.com/news/articles/2020-10-22/saba-s-boaz-weinstein-predicts-credit-chaos-around-u-s-election



0 Comments